magnétostatique (suite)

L’équation de Poisson et l’équation de Laplace de la magnétostatique du vide

À partir des relations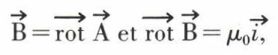

on établit l’équation de Poisson du potentiel-vecteur

dans une région où il n’y a pas de courants, cette équation prend la forme de l’équation de Laplace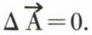

De même, à partir des relations

valables en dehors des courants, on établit l’équation de Laplace du potentiel scalaire magnétique ΔV = 0.

Avec ces équations, l’étude du champ du vecteur induction magnétique se ramène à celle de l’étude du champ électrique en électrostatique. Il suffit d’exprimer les solutions particulières de ces équations en tenant compte des conditions aux limites et de déterminer en prenant les composantes de ou bien celles de

Le dipôle magnétique

Certains circuits électriques présentent des propriétés intéressantes pour la compréhension des phénomènes physiques. C’est le cas du circuit représentant le dipôle magnétique. Il s’agit d’une spire de petite dimension (fig. 6), parcourue par l’intensité I, et définissant l’élément de surface dS autour du point O.

Du point M du vide extérieur, cette spire est vue sous l’angle solide

et l’induction en M dérive du potentiel scalaire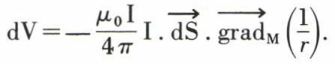

Cette expression a la même forme que celle qui est relative au potentiel du dipôle électrique. Par analogie, on définit le moment du dipôle magnétique par l’expression

En poursuivant la comparaison, on peut définir la masse magnétique ponctuelle, homologue de la charge électrique. Le dipôle magnétique peut ainsi être représenté par deux masses magnétiques, + m et – m, à la distance dl, de telle sorte que le moment soit égal à 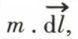le vecteur étant orienté de – m vers + m. La loi de Coulomb peut alors être appliquée à ces masses magnétiques.

Bien qu’apparaissant formellement par équivalence avec l’électrostatique, la théorie a confirmé la possibilité d’existence de la masse magnétique ; on lui a donné le nom de monopôle ; les tentatives pour découvrir cette particule ont jusqu’alors été infructueuses.

Magnétostatique des milieux matériels

La loi de Biot et Savart dans un milieu matériel

Si l’on répète l’expérience d’Ampère dans différents milieux, gazeux ou liquides par exemple, on observe que l’amplitude des forces de Laplace est différente. Or, la forme même de la loi de Laplace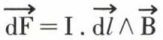

ne fait pas référence au milieu ; il est donc nécessaire que l’induction dépende du milieu. Pour rendre compte de cette propriété, on exprime la loi de Biot et Savart sous la forme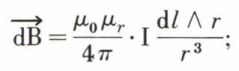

elle diffère de l’expression établie dans le vide par le coefficient μ_r qui dépend du milieu et que l’on nomme perméabilité magnétique relative de la matière. Ce coefficient μ_r caractérise la modification de la matière produite par les courants circulant dans les conducteurs.

Polarisation de la matière

Le mécanisme physique à l’origine de la polarisation de la matière est d’ordre atomique ; son étude dépasse le cadre de cet article ; disons simplement que certains atomes possèdent un moment permanent, analogue au moment d’un dipôle, que, pour les autres, un champ induit un moment et que le résultat de l’application du champ est l’apparition d’un moment macroscopique dans tout le volume de l’échantillon de matière ; c’est la propriété de polarisation de la matière.

Supposons la polarisation uniforme ; désignons par le moment par unité de volume, ou intensité d’aimantation ; l’élément de moment correspondant à un élément de volume dv est

il a les propriétés du moment d’un dipôle, et un observateur ne peut discerner si ce moment est dû à de la matière polarisée ou bien produit par les courants. En utilisant les résultats obtenus lors de l’étude du dipôle, on écrit que l’induction magnétique en un point M dérive du potentiel scalaire

suivant l’expression

On ramène l’étude de la magnétostatique des milieux matériels à celle de la magnétostatique des courants dans le vide en déterminant la répartition des courants qui créent la même induction On passe par l’intermédiaire du potentiel-vecteur ; on exprime de telle manière que pour un volume v de matière délimité par la surface S.

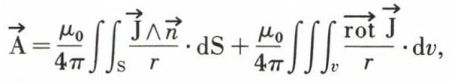
désignant la normale unitaire positive à la surface S.

Les deux termes au second membre sont analogues aux expressions du potentiel-vecteur établi en magnétostatique du vide ; on conclut que le volume polarisé est équivalent à une répartition en volume de courant, avec la densité et à une répartition en surface, avec la densité Ces courants équivalents sont appelés courants ampériens.

Pour un cylindre de matière polarisé uniformément avec l’intensité d’aimantation , la densité de courant ampérien en volume est nulle, et la densité en surface est égale à J ; c’est un vecteur tangent au cylindre et dans un plan perpendiculaire à son axe.

Les équations locales de l’induction magnétique 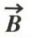et du champ magnétique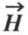

On remplace le système « courants réels et matière aimantée » par le système « courants réels et courants ampériens » ; on attribue aux courants ampériens les mêmes propriétés magnétostatiques qu’aux courants réels ; on peut alors exprimer le potentiel-vecteur résultant en chaque point et déduire l’induction par la relation

Il est clair que la condition 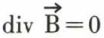est toujours valable, c’est-à-dire que le flux de à travers une surface fermée, même traversant la matière aimantée, est nul.