magnétostatique (suite)

Le théorème d’Ampère s’écrit

en désignant par la densité de courant résultante ; dans le cas le plus général, cette densité est la somme de la densité de courant réel et de la densité des courants ampériens ; à l’intérieur du milieu magnétique, cette relation d’Ampère s’écrit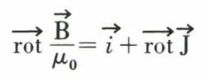

ou encore

On définit alors le vecteur champ magnétique 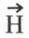dans la matière aimantée par la relation

cette définition permet d’écrire le théorème d’Ampère dans la matière aimantée par la relation

la même que celle qui est établie en magnétostatique des courants dans le vide.

On exprime alors l’induction dans la matière aimantée par la relation

Les définitions de et 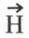fournissent une correspondance entre l’induction magnétique et le champ électrique 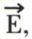d’une part, et entre le champ magnétique 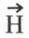et l’induction électrique d’autre part. Avec les vecteurs du premier groupe, on exprime les forces ; les vecteurs du second groupe donnent une correspondance entre les sources et les champs.

Dans la pratique, on mesure le moment magnétique en fonction du champ magnétique 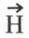 ; celui-ci est connu à partir des courants. Nous avons reproduit (fig. 7) la courbe d’aimantation d’une sphère de cobalt en fonction du champ à la température ambiante et (fig. 8) la courbe d’induction du fer.

Le rapport est la perméabilité absolue μ du milieu. Lorsque celui-ci est paramagnétique, l’aimantation est proportionnelle au champ, J = χH, avec χ désignant la susceptibilité ; dans ces conditions
B = μ₀(1 + χ)H ;
on voit ainsi apparaître le terme de perméabilité relative μ_r que nous avons introduit précédemment dans l’expression de la loi de Biot et Savart. D’une manière générale, la perméabilité absolue μ est égale à μ₀μ_r.

Dans un milieu matériel, l’équation de Poisson du potentiel-vecteur s’écrit alors

elle se réduit à l’équation de Laplace 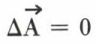lorsqu’il n’y a pas de courants réels.

Toujours en l’absence de courants réels, on peut écrire, compte tenu de l’équivalence entre la matière polarisée et les courants ampériens, que l’induction dérive du potentiel scalaire V, ce dernier satisfaisant à l’équation de Laplace ΔV = 0.

Polarisation d’une sphère magnétique placée au centre d’un solénoïde

Avant l’introduction de l’échantillon, l’induction B₀ et le champ H₀ au centre du solénoïde sont uniformes. L’introduction de l’échantillon modifie le tracé des lignes de force.

Comme aucun courant ne circule à l’intérieur du solénoïde et dans l’échantillon, l’induction dérive du potentiel scalaire V, satisfaisant à l’équation de Laplace.

La solution générale de ΔV = 0, dans la symétrie considérée, est connue ; la solution particulière est définie en tenant compte des conditions aux limites à la surface de la sphère, à savoir qu’il y a conservation de la composante normale de l’induction et conservation de la composante tangentielle du champ.

Le calcul montre que le champ à l’intérieur de la sphère H_i est uniforme (fig. 9) ; il s’exprime en fonction du champ H₀ par la relation

La polarisation de la sphère est donc uniforme. H_i est toujours inférieur à H₀ ; la différence H₀ – H_i représente un champ qui tend à désaimanter la substance : c’est le champ démagnétisant H_d, qui s’exprime simplement en fonction de l’intensité d’aimantation par la relation vectorielle

Énergie magnétostatique

Nous envisageons les deux cas importants suivants :
1. Dans une région de l’espace, l’induction est créée par des sources extérieures fixes. Un circuit parcouru par le courant d’intensité I est déplacé d’une région de l’espace où l’induction est nulle vers une région où règne l’induction . Les forces de Laplace sur le conducteur imposent de fournir un travail qui est donné par l’expression IΦ, Φ étant le flux de dans le circuit dans sa position finale. L’énergie du circuit dans l’induction extérieure est prise égale à zéro dans la région où B = 0 ; elle est égale à W = – IΦ dans l’état final.
Pour un dipôle magnétique, cette énergie s’écrit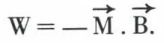

2. Lorsque le système dont on veut exprimer l’énergie comprend également les sources de champ, le problème est plus délicat ; en effet, la réalisation d’un état final statique des courants et des champs associés nécessite un fonctionnement en régime transitoire pendant un certain temps ; des champs variables existent, et des forces électromotrices apparaissent ; elles imposent aux sources de courants de fournir un travail.

Pour un système de courants répartis dans un volume v avec la densité en présence ou non de matière polarisée, la variation d’énergie magnétique pendant l’intervalle de temps δt est

cette relation s’exprime encore en fonction des champs 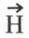et sous la forme

l’intégrale étant étendue à tout l’espace. Elle indique que l’énergie est localisée dans l’espace.

Pour un système de courants isolés, l’énergie magnétique est

on déduit de cette expression l’énergie propre d’un circuit

Φ étant le flux dans ce circuit de l’induction créée par l’intensité I y circulant ; c’est encore

L désignant le coefficient d’inductance du circuit.

Pour un milieu magnétique linéaire, l’énergie s’écrit

Pour un milieu ferromagnétique avec hystérésis, l’énergie du système dépend de l’état d’aimantation du milieu sur le cycle d’hystérésis.

Conclusion

De cet article, il ressort que les phénomènes magnétostatiques sont associés aux courants électriques, c’est-à-dire au mouvement des électrons, ou encore à la circulation de la matière. En fait, les phénomènes magnétostatiques représentent un domaine particulier des phénomènes électromagnétiques, qui apparaissent lorsque des milieux matériels sont en mouvement relatif. L’unification de ces propriétés avec les propriétés électriques est donnée par la théorie de la relativité.

R. P.

 E. Durand, Magnétostatique (Masson, 1968).