logique combinatoire

Partie de la logique mathématique qui a pour objet ses fondements ultimes. C’est une sorte de « protologique ».

Introduction

L’une des façons de caractériser un calcul logique consiste en la donnée d’un système d’axiomes, accompagné de certaines règles. Parmi elles figurent nécessairement des règles de substitution. Dans le cas des systèmes simples, calcul des propositions par exemple (v. calcul des propositions), la formulation des règles de substitution est relativement aisée. Il en va tout autrement dans les systèmes plus complexes, comme dans le calcul des prédicats. En fait, les difficultés y sont telles qu’il a fallu attendre 1935-36 pour en avoir une formulation correcte. Un des obstacles est constitué par la présence de variables au sein des formules logiques et mathématiques.

Si l’on écrit, par exemple, en arithmétique, x + 0 = x, on ne communique aucune information sur x, mais seulement sur l’addition et sur zéro. De même, une expression logique comme p ⊃ (q ⊃ p) ne renseigne ni sur p ni sur q, mais seulement sur la conditionnelle (⊃). On peut donc estimer que l’usage de variables a un caractère assez peu naturel, surtout si l’on est encore amené à distinguer entre variables libres et liées (v. calcul des prédicats). On peut songer en conséquence à s’en passer entièrement. Notons aussi que le passage en mathématiques d’écritures de la forme y = f (x) à la notation des applications f : E → F répond à la même préoccupation.

L’une des tâches de la logique combinatoire due à Curry — et d’autres « logiques », comme celle dite « de la λ-conversion », due à Church — est d’élucider ces problèmes de variables et de substitution. Mais ce n’est pas la seule. La découverte des antinomies, et en particulier celle de Russell (v. classe et relation), a réclamé une analyse des diverses catégories que constituent les objets logiques. Il fallait expliquer pourquoi, si x ∈ α . ≡ . ~ (x ∈ x) peut être considéré comme une proposition, α ∈ α. ≡ ~ (α ∈ α) ne le peut pas. L’étude de ces phénomènes est une autre tâche de la logique combinatoire.

Les combinateurs I, W, K, C, B

Partons d’une expression logique quelconque, par exemple de

et donnons-nous une règle qui autorise à substituer des expressions bien formées aux variables de propositions.

Alors, en substituant p à q dans (1), on aura

En substituant (p ⊃ p) à q dans (1), il vient

En substituant p à q et q à p dans (1), on a

D’un point de vue purement extérieur, le passage de (1) à (2) a eu comme effet de supprimer la mention de q ; celui de (1) à (3), de supprimer la mention de q et d’augmenter le nombre des mentions de p ; celui de (1) à (4), de permuter l’ordre des mentions de p et de q. De là l’idée qu’un petit nombre d’opérations tout à fait élémentaires allaient permettre une description et une analyse précises des opérations de substitution.

À chacune de ces opérations élémentaires va correspondre un opérateur bien défini, appelé combinateur. Nous allons donner une description intuitive des principaux.

Soit des objets, pour le moment entièrement quelconques, mais dont nous distinguerons certains. Les objets distingués seront des lettres majuscules, les autres des lettres minuscules.

Soit I un premier objet distingué, appelé identificateur. Nous poserons que la suite Ia peut se récrire a :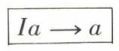

Soit de même W, appelé répétiteur, et tel que :

Supposons que m soit la multiplication, x et y des nombres. Alors mxy est une façon de noter le produit de x par y. La chaîne Wmx se récrit mxx et désigne en conséquence le carré de x.

Introduisons K, appelé éliminateur, par la condition :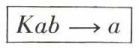

Comme nos objets sont indéterminés, on pourra avoir par exemple : KIa → I.

Soit encore C le permutateur.

En reprenant l’exemple de la multiplication, on aura Cmxy → myx.

Pour saisir la portée de l’objet B, dit compositeur, considérons la fonction numérique f = df le triple de et g = df le carré de. On aura par exemple :

Convenons d’écrire simplement fx et gx au lieu de la notation usuelle f (x) et g(x). On aura ainsi :
f 4 = 12, f 6 = 18, g 2 = 4, g 6 = 36, etc.
Mais ici surgit une difficulté. Si f 4 = 12, on a aussi 4 = g 2. Toutefois, comme f est une fonction à un seul argument, l’écriture fg 2 n’a pas de sens. Dès lors, pour exprimer l’idée :
f pour la valeur que prend g pour 2,
nous noterons : f (g 2). Entourer g 2 d’une paire de parenthèses revient à obtenir un seul objet. De là le compositeur B :

On peut écrire : Bfgx → f (gx).

En résumé, si l’on considère les combinateurs I, W, K, C, B comme des opérateurs, on peut dire :

On peut noter que les combinateurs ci-dessus laissent tous leur premier argument invariant. On les dit normaux.

Il est clair qu’un combinateur, appliqué à un nombre d’arguments inférieur à celui qui est requis, n’a pas d’« effet » : nous ne savons pas récrire la chaîne Ka. En revanche, nous allons postuler que les règles de récriture restent valables indépendamment des objets qui suivent ou qui précèdent.

Exemples.
1. Wabcd → abbcd ;
2. CIab → Iba → ba.
Soit X et Y deux combinateurs. Disons qu’ils sont égaux, et notons X = Y, s’ils ont le même effet. Ainsi, I = WK, puisqu’on a
Ia → a et WKa → Kaa → a.
Si l’on pose T = df CI, l’exemple 2 montre qu’il existe des combinateurs non normaux.