logique combinatoire (suite)

Introduisons un combinateur S, tel que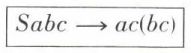

A lui seul, S a trois « effets » : il double un de ses arguments (c), il permute l’ordre (c est récrit avant b) et il compose deux arguments. Il est donc plausible que tous les combinateurs introduits plus haut puissent se définir à l’aide de S et K seulement. Vérifions la chose, tout en notant que nous convenons de supprimer toute paire de parenthèses qui vient se situer en tête d’une chaîne ou en tête d’une sous-chaîne.

I = SKK.
En effet :
SKKa → Ka(Ka) → a.

W = SS(SK).
En effet :
SS(SK)ab → Sa(SKa)b → ab(SKab) → abKb(ab) → abb.

B = S(KS)K.
En effet :
S(KS)Kabc → KSa(Ka)bc → S(Ka)bc → Kac(bc) → a(bc).

C = S(BBS)(KK).
En effet :

Une axiomatisation de la théorie des combinateurs peut donc se faire à l’aide de S et K pris comme primitifs.

Il est naturel de se demander s’il n’est pas possible de réitérer l’effet d’un combinateur. Le problème a une solution simple dans le cas des combinateurs normaux.

Soit à trouver X tel que Xab → abbb.

Si l’on applique W à abb, on aura la chaîne souhaitée : Wabb → abbb. Toutefois, si on réapplique W à Wabb, on obtient WWabb → Waabb, ce qui n’est pas l’effet désiré. Cela découle de ce que W agit sur son deuxième argument. Si l’on avait (Wa)b au lieu de Wab, il viendrait :
W(Wa)b → Wabb → abbb.
Il suffit donc, avant d’utiliser de nouveau W, de lier Wa par B. On aura donc : X = BWW.

En effet : BWWab → W(Wa)b → Wabb → abbb.

On est ainsi conduit à définir la notion de puissance d’un quantificateur de la façon suivante : si X et Y sont deux combinateurs normaux, alors
X.Y = df BXY ;
X¹ = df X ;
X² = df X.X ;
X³ = df X².X ; etc.
On peut donc écrire : W² = df BWW.

On voit que :
Iⁿ = I ;
Wⁿ répète n fois le 2^e argument, qui est donc écrit n + 1 fois ;
Kⁿ supprime n arguments à partir du 2^e (lui compris) ;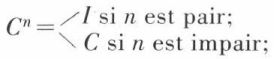

Bⁿ lie n arguments au 2^e, donc on place n + 1 entre parenthèses.

Exemples
1. K³abcdef → aef.
En effet, on a par les définitions :
K³ = K².K = (K.K).K = (BKK).K = B(BKK)K.
Dès lors :

On remarquera que les parenthèses qui ne sont pas en tête doivent être conservées.

2. (K³.W²)abcdef → aeeef.
En effet : K³.W² = BK³W². Donc
BK³W²abcdef → K³(W²a)bcdef → W²aef → aeeef.
On notera la commodité de l’opération produit (marquée par un point) : les combinateurs agissent successivement. Ainsi, on a la chaîne abcdef. On fait agir K³ et on obtient la chaîne aef, sur laquelle on fait agir W².

Il reste à examiner comment faire agir un combinateur donné à distance, c’est-à-dire après la deuxième place. Toujours dans le cas des combinateurs normaux, autre que I, on voit que c’est encore B et ses puissances qui offrent une solution. En effet, si X est normal, on peut écrire :
Xx₁x₂...x_n → x₁y₁y₂...y_m.
Dans ces conditions,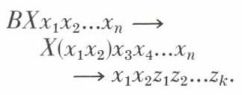

En conséquence, BⁱX fait agir X à partir de son (i + 2)^e argument.

Exemple.
B³K² chatte → chat.
En effet :
B³ = B².B = (B.B).B = B(B.B)B = B(BBB)B.
Donc : B³K² = B(BBB)BK².
Et il vient :
B(BBB)BK² chatte → BBB(BK²) chatte → B(B(BK²)) chatte → B(BK²) (ch)atte.
→ BK²(cha)tte → K²(cha)te → chat.

On conçoit que de tels mécanismes permettent de rendre compte des substitutions. Voyons, par exemple, comment passer de l’expression (1) p ⊃ (q ⊃ p) à l’expression obtenue en substituant (p ⊃ p) à q, soit à (2) p ⊃ ((p ⊃ p) ⊃ p).

Commençons par éviter les parenthèses dans ces deux formules et posons que, d’une façon générale, α ⊃ β se notera : c α β. On aura donc
(1) cpcqp et (2) cpccppp.
Les minuscules sont assimilées à nos objets et le problème se ramène à trouver un combinateur X tel que
Xcpcqp → cpccppp.
Il est possible de prendre X = B²K.BW.B²W², par exemple, mais la solution n’est pas unique. Nous avons, en effet, la chaîne initiale cpcqp. Appliquons B²K, qui supprime le 4^e argument. On trouve cpcp. Appliquons BW, qui répète le 3^e argument. On a cpccp. Si on applique enfin B²W², qui répète deux fois le 4^e argument, on trouve cpccppp, ce qui est le résultat de la substitution.

La fonctionnalité

Admettons que les objets que l’on veut étudier se répartissent en diverses catégories : α, β, γ, etc. Si l’objet x appartient à la catégorie α, nous écrirons x ∈ α. Soit alors un opérateur binaire entre catégories, noté F et lu « flèche ». Nous poserons la règle unique :
si ab ∈ α et b ∈ β, alors a ∈ Fβα,
qu’il est possible d’écrire plus commodément sous la forme :

Cela signifie que, si la chaîne ab appartient à la catégorie α et b à la catégorie β, a appartient à la nouvelle catégorie Fβα.

Exemple.

Si a et b sont deux nombres naturels, leur produit, que nous noterons encore mab, est un nombre naturel. À quelle catégorie appartient l’opérateur m ? Soit ℕ la catégorie des nombres naturels. Une double application de la règle ci-dessus donne :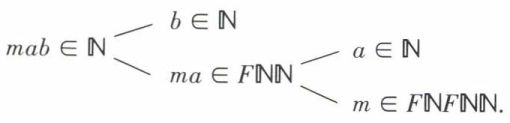

Si l’on note [x] la catégorie à laquelle appartient en particulier x, on a :

C’est-à-dire que, si a, b, mab ∈ ℕ, alors ma ∈ Fℕℕ et m ∈ FℕFℕℕ.

Pour appliquer ce genre d’analyse à la logique, donnons-nous deux catégories primitives : celle des objets ω et celle des propositions π. Si x₁ est un objet et si a est un prédicat à une place (propriété), ax₁ est une proposition (v. calcul des prédicats). La règle ci-dessus nous permet d’écrire :

Un prédicat unaire appartient à la catégorie « flèche de ω à π » :

En d’autres termes, un prédicat unaire est ce qui, appliqué à un objet, engendre une proposition.

Un prédicat binaire r (une relation) donne lieu à l’analyse représentée par le schéma :

Exemple.
rx₁x₂ = df x₁ est plus petit que x₂.

Dès lors rx₁, soit « x₁ est plus petit que », appartient à la catégorie Fωπ, donc à la catégorie des propriétés, et r à la catégorie FωFωπ, soit à la catégorie des relations (binaires).

Si l’on veut exprimer que la relation r est asymétrique, on pourra noter Asym r (v. classe et relation) et on aura :

On voit intuitivement par ces quelques exemples que l’opérateur F permet de répartir en catégories tous les « objets » qui figurent dans les calculs logiques.