groupe (suite)
Sous-groupe d’un groupe
On appelle ainsi toute partie H d’un groupe G telle que la restriction de la loi de G à H soit une loi de groupe. Les éléments neutres de G et H, e et є, sont égaux, car єє = є ; d’où є = єє–1 = e. Par suite, le symétrique d’un élément est le même dans H et dans G ; d’où H–1 ⊂ H (H–1, ensemble des symétriques des éléments de H). D’autre part, H est une partie stable de G ; d’où HH ⊂ H (HH, ensemble des produits d’un élément quelconque de H par un élément quelconque de H).
Inversement, toute partie H de G telle que H–1 ⊂ H et HH ⊂ H est stable ; dès qu’elle contient x, elle contient x–1 ; donc xx–1 = e, qui est neutre ; comme la loi reste associative sur H, H est un sous-groupe de G. On voit, d’ailleurs, que HH = H et H–1 = H. On peut résumer ces propriétés caractéristiques d’un sous-groupe H de G par la condition nécessaire et suffisante suivante : pour x et y dans H non vide, x y–1 ∈ H. Cette condition est visiblement nécessaire. Elle est suffisante, car elle entraîne e ∈ H pour y = x, puis H–1 ∈ H pour x = e et enfin x z ∈ H ou HH ⊂ H pour y = z–1.
Exemples de sous-groupes. 1. Dans le groupe additif ℤ des entiers relatifs, tout sous-ensemble de la forme a ℤ, a ∈ ℤ, est un sous-groupe.
2. Dans l’ensemble des déplacements du plan (groupe des translations-rotations), les translations forment un sous-groupe ; de même les rotations de centre donné.
3. Dans le corps ℂ des nombres complexes, l’ensemble ℂ* des complexes non nuls est un groupe multiplicatif. Le sous-ensemble des complexes de module 1 est un sous-groupe multiplicatif.
Sous-groupe distingué
Le sous-groupe H du groupe G est un sous-groupe distingué si aHa–1 = H pour tout a de G.
Il suffit de vérifier que, pour tout a de G, il existe x ∈ H tel que a x a–1 ∈ H. Cela revient à dire que H est distingué s’il est conservé par tout automorphisme intérieur. En effet, la transformation f qui à x associe y = axa–1 est un isomorphisme de G sur G ou une application biunivoque de G sur G, qu’on appelle automorphisme intérieur.
Relations d’équivalence et groupes quotients
Si H est un sous-groupe distingué d’un groupe G non nécessairement abélien, on définit la relation suivante :
x ℛ y ⇔ x y–1 ∈ H.
On vérifie qu’elle est réflexive, transitive et symétrique ; c’est donc une relation d’équivalence. La classe d’équivalence de l’élément neutre e est fournie par x e–1 ∈ H, soit x ∈ H ; c’est le sous-groupe H. La classe d’équivalence de l’élément a est donnée par x a–1 ∈ H ou x ∈ H a ; c’est le complexe Ha ou translaté à droite de H, ou simplement translaté, puisque 
(H est distingué).
Cette relation ℛ a une propriété fort importante : elle est compatible avec la loi du groupe G. En effet
x ℛ y ⇔ x y–1 ∈ H ⇒ x a a–1 y–1 ∈ H,
car a a–1 = e ou x a (ya)–1 ∈ H ⇔ x a ℛ y a ;
d’où la compatibilité à droite, puisque
x ℛ y ⇒ x a ℛ y a.
Mais on a aussi a x ℛ a y,
car a x y–1 a–1 ∈ H,
puisque x y–1 ∈ H et que a H a–1 = H.
D’où la compatibilité de ℛ avec la loi de G. Les classes d’équivalence sont les translatés aH = Ha.
Groupe quotient
L’ensemble quotient G/ℛ de G par ℛ, c’est-à-dire l’ensemble de toutes les classes d’équivalence, G/ℛ = {a H, a ∈ G}, noté aussi G/H, est doté d’une structure de groupe. On peut, en effet, définir une loi de composition interne sur les classes, car si x et y sont des représentants des deux classes X et Y, la classe Z de xy dépend de X et de Y, et non des représentants choisis ; on note donc Z = X . Y ; d’où la loi de composition interne sur G/H, qui est une loi de groupe ; G/H est le groupe quotient de G par H.
Cas particulier. Si G est fini, H est nécessairement fini, puisque H ⊂ G. Tous les translatés aH contiennent le même nombre d’éléments que H. Donc l’ordre de H divise celui de G.
Ce résultat s’applique d’ailleurs aux cas où H n’est pas distingué, la relation ℛ étant simplement compatible à droite ou à gauche avec la loi de G. Si G est d’ordre p premier, G n’admet aucun véritable sous-groupe : les seuls sous-groupes sont G et {e}.
Exemple de groupe quotient. Dans l’ensemble ℤ des entiers relatifs, qui est un groupe additif, tout sous-groupe est distingué et de la forme a ℤ, où a ∈ ℕ*. Le groupe quotient ℤ/aℤ est l’ensemble des entiers modulo a. La relation d’équivalence ℛ est définie par x ℛ y ⇔ x – y ∈ a ℤ ou
x – y = a k, k ∈ ℤ.
On voit que ℤ/aℤ contient a éléments en formant successivement les classes des éléments 0, 1, ..., a – 1 et a, dont la classe est confondue avec celle de 0. On peut alors confondre les classes avec leurs représentants 0, 1, ..., a – 1 et calculer sur les classes (vis-à-vis de l’addition) comme sur les représentants. Par exemple, pour a = 5, 
la barre indiquant la classe du nombre qu’elle surmonte ; on peut prendre comme représentants {0, 1, 2, 3, 4} et former la table d’addition de ℤ/5ℤ ; par exemple : 2 + 4 = 6, 6 ℛ 1, d’où 
d’où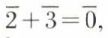 
car 5 ℛ 0 ; 
sont donc inverses l’un de l’autre, etc. La notion de groupe quotient est importante : elle fournit un procédé d’obtention de nouveaux groupes à partir de groupes donnés.
Groupe monogène ; groupe cyclique
Un groupe est monogène lorsqu’il est engendré par un seul élément : {e, a, a2, ..., an, ...}, n ∈ ℤ ; le groupe est noté (a).
Un groupe est cyclique s’il est monogène et fini : (a) = {e, a, a2, ..., an–1} et an = e ; par exemple, le groupe des racines n-ièmes de l’unité données par
est un groupe cyclique.
• Pour que ap engendre le groupe cyclique (a) d’ordre n, il faut et il suffit que p et n soient premiers entre eux : (p ⌒ n) = 1 ; par suite, si n est premier, ap engendre (a) pour tout p tel que 0 < p < n.
• Tout sous-groupe d’un groupe cyclique est cyclique.