fonction réelle d’une ou plusieurs variables réelles (suite)
Exemples.
par application itérée de la deuxième règle.
d’où 
(application de la dernière règle).
Formule de Taylor. Si f admet des dérivées continues jusqu’à l’ordre n sur [a, b] et une dérivée d’ordre n + 1 dans ]a, b[, on a
Cette formule permet des développements limités ou des développements en série entière au voisinage d’une valeur a, sous certaines réserves. Par exemple,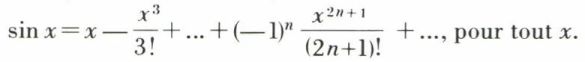
Appliquée au premier ordre, la formule de Taylor prend la forme de formule des accroissements finis :
f(b) – f(a) = (b – a) f ′(c), avec a < c < b ;
elle est applicable à une fonction seulement continue sur [a, b] et dérivable sur ]a, b[.
Application de la dérivée au sens de variation d’une fonction. Ce sens de variation est donné par le signe de la dérivée : si une fonction f définie sur [a, b] y a une dérivée de signe constant, sauf en des points isolés où la dérivée peut être nulle, elle est croissante si la dérivée est positive et décroissante si la dérivée est négative.
L’étude complète d’une fonction f consiste à déterminer :
— le domaine de définition D ;
— les limites de la fonction aux bornes de D ;
— la dérivée f ′ et son signe, ce qui partage D en intervalles partiels où f est monotone (constamment croissante ou constamment décroissante) ;
— une représentation graphique, qui exige en général l’étude de branches infinies, de tangentes aux points d’arrêt et de points d’inflexion.
Fonction de plusieurs variables réelles
C’est l’application d’une partie de ℝn dans ℝ. Les cas les plus fréquents sont n = 2 et n = 3.
Exemples. 
est une application de ℝ2 – (0, 0) dans ℝ.
est une application de la partie de ℝ3 non intérieure à la sphère de centre 0 et de rayon 2 dans ℝ+ (ensemble des réels positifs).
Pour 
une fonction de plusieurs variables peut être assimilée à une fonction de point u = f(M), les variables, au nombre de n, étant considérées comme les coordonnées du point M. Pour n = 2, z = f(x, y) = f(M) définit une surface de l’espace ℝ3 dont l’équation est précisément z = f(x, y) ; cela permet une interprétation géométrique de certains résultats concernant la fonction f, notamment sur les dérivées partielles.
Limite. Continuité. La fonction de point u = f(M) est continue au point M0 de son domaine D si, quand M tend vers M0, sur D, f(M) tend vers f(M0). Une fonction continue de plusieurs variables est continue séparément par rapport à chaque variable. Mais il n’est pas suffisant qu’une fonction soit continue par rapport à chaque variable pour être continue par rapport à l’ensemble des variables.
Dérivée partielle. C’est la dérivée par rapport à une des variables, les autres variables étant considérées comme constantes. Par exemple, pour u = f(x, y, z), on définit, quand cela est possible, trois dérivées partielles notées
On définit aussi, si possible, des dérivées partielles d’ordre supérieur (secondes, troisièmes, etc.) :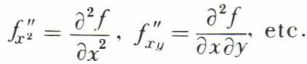
Si 
sont définies et continues, on a d’ailleurs 
On peut considérer les dérivées partielles 
comme les composantes, en axes orthonormés, du vecteur normal à la surface d’équation f(x, y, z) = 0 au point (x, y, z).
Dérivée d’une fonction composée. Si f(u, v, w) est une fonction composée de x et de y par l’intermédiaire de u (x, y) et de v (x, y), on a sous certaines hypothèses :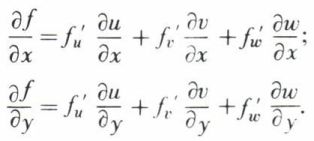
E. S.
➙ Application / Calcul numérique / Différentielle / Espace / Intégrale / ℝ / Suite / Topologie.
A. Hocquenghem et P. Jaffard, Mathématiques, t. I (Masson, 1962 ; 3e éd., 1967). / G. Casanova, Mathématiques spéciales, t. II : Algèbre et analyse (Berlin, 1964). / J. Lelong-Ferrand et J.-M. Arnaudiès, Cours de mathématiques, t. II, Analyse (Dunod, 1972).
Quelques grands noms de la théorie des fonctions
Lazarus Fuchs,
mathématicien allemand (Moschin, Prusse, 1833 - Berlin 1902). Disciple de Karl Weierstrass (1815-1897), professeur à Heidelberg, puis, à partir de 1884, à Berlin, où il succéda à son maître, il s’est surtout intéressé aux équations différentielles linéaires. Ses recherches ont influencé les travaux d’Henri Poincaré (1854-1912), qui a donné le nom de groupe fuchsien à un groupe de transformation du plan et celui de fonctions fuchsiennes à des fonctions de la variable complexe invariantes pour ce groupe.
Édouard Goursat,
mathématicien français (Lanzac 1858 - Paris 1936). Élève de l’École normale supérieure en 1876, agrégé préparateur en 1879, Goursat soutient en 1881 une thèse sur l’équation différentielle, admettant pour intégrale la fonction hypergéométrique. Professeur à l’université de Toulouse de 1882 à 1885, puis maître de conférences à l’École normale, il succède en 1897 à Émile Picard à la Sorbonne, où il enseigne le calcul différentiel et intégral, puis l’analyse supérieure. Ses travaux d’analyse portent surtout sur les équations aux dérivées partielles du second ordre, dont il formule une classification. Son Cours d’analyse mathématique, remarquable par sa clarté et sa vaste documentation, a eu une influence heureuse sur plusieurs générations de mathématiciens. (Acad. des sc., 1919.)
Émile Picard,
mathématicien français (Paris 1856 - id. 1941). Élève de l’École normale supérieure, où il a pour maîtres Gaston Darboux (1842-1917), Charles Briot (1817-1882) et Claude Bouquet (1819-1885), il est, à vingt et un ans, agrégé et docteur. Après quelques travaux remarquables de géométrie, il se tourne vers l’analyse. Il établit en 1879 un théorème resté célèbre : Au voisinage d’un point singulier essentiel isolé, toute fonction analytique de la variable complexe prend une infinité de fois toute valeur, sauf au plus deux. Il professe à la faculté des sciences de Toulouse, puis à Paris à partir de 1881. Il se livre à des recherches sur les fonctions uniformes de deux variables complexes et fait connaître ses fonctions hyperfuchsiennes et hyperabéliennes (1883-84). Il découvre un groupe de transformations des points de l’espace que Félix Klein (1849-1925) appellera « groupe de Picard ». Ses travaux sur les équations différentielles se fondent sur la théorie des groupes, qu’Evariste Galois (1811-1832) avait créée pour l’étude des équations algébriques. (Acad. des sc., 1889.)
Michel Rolle,