élasticité (suite)

Sur la face perpendiculaire à ox passant par M, la force est X₁ dy dz ; sur la face parallèle à la distance dx, la force est

elle est dirigée en sens contraire de la précédente. Leur somme algébrique est donc

L’équilibre du parallélépipède élémentaire s’obtient en écrivant d’abord

En divisant par dx dy dz, on a
de même, par permutation, on obtient :
mais l’équilibre du parallélépipède exige aussi que la somme des moments par rapport aux axes soit nulle.
Les contraintes X₁Y₁Z₁ deviennent N₁T₃T₂.
Les contraintes X₂Y₂Z₂ deviennent T₃N₂T₁.
Les contraintes X₃Y₃Z₃ deviennent T₂T₁N₃.
Les quantités N₁N₂N₃ étant les composantes normales de contraintes sur les plans perpendiculaires aux axes et les quantités T₁T₂T₃ les composantes tangentielles, le système des trois équations (I) précédentes devient :

On a donc six fonctions de trois variables liées par trois équations différentielles.

• Équilibre du tétraèdre élémentaire. Déterminons la contrainte attachée à un élément plan ABC infiniment voisin d’un point M d’un corps et défini par ses cosinus directeurs α, β et γ.
Soit dS l’aire de ce triangle ABC et X, Y, Z les composantes de la contrainte associée au plan oblique ABC ; les composantes de la force exercée sur ABC seront
X dS, Y dS et Z dS.
Les composantes de la force exercée sur la base MBC d’aire α dS seront
— N₁ α dS, — T₃ α dS et — T₂ α dS.
Les composantes de la contrainte sur la face AMC d’aire β dS seront
— T₃ β dS, — N₂ β dS et— T₁ β dS.
Enfin, les composantes de la contrainte sur la face MAB d’aire γ dS seront
— T₂ γ dS, — T₁ γ dS et — N₃ γ dS.
En égalant à zéro la somme des composantes relatives à chacun des axes et en divisant par dS, on obtient le système d’équations :

Si l’on porte du point M un vecteur contrainte, l’ensemble des extrémités de ces vecteurs définit l’ellipsoïde de Lamé, ou ellipsoïde des contraintes ; les composantes du vecteur étant X, Y, Z, on obtient l’équation de l’ellipsoïde de Lamé en éliminant α, β, γ entre, d’une part, les trois équations (II), qui sont linéaires, et, d’autre part, la relation reliant α, β et γ, c’est-à-dire
α² + β² + γ² = 1.
De l’étude de l’équilibre du tétraèdre élémentaire, on déduit qu’une contrainte (associée à un plan quelconque passant par un point du corps), de composantes (X, Y, Z), est entièrement connue si l’on connaît les contraintes pour trois plans rectangulaires quelconques et en particulier les trois contraintes principales, définies par les trois axes de l’ellipsoïde de Lamé.

Les contraintes (X, Y, Z) autour d’un point, pour tous les éléments de surface passant en ce point, sont complètement déterminées par la connaissance des six quantités N₁ N₂ N₃ T₁ T₂ T₃ au moyen des formules :
X = α N₁ + β T₃ + γ T₂,
Y = α T₃ + β N₂ + γ T₁,
Z = α T₂ + β T₁ + γ N₃,
α, β et γ étant les cosinus directeurs de (X, Y, Z).

Relations entre les contraintes et les déformations. Cas des corps isotropes et homogènes

Le problème consiste à chercher les relations qui existent entre, d’une part, les forces N et T et, d’autre part, les déformations. En supposant très faibles les déplacements (u, v, w) et également leurs variations quand on passe d’un point au point voisin, on peut, dans les déformations, n’introduire que les déplacements (u, v, w) et leurs dérivées partielles du premier ordre, soit

Dans le cas des corps isotropes, les coefficients qui interviennent pour relier entre elles les contraintes et les déformations sont réduits à deux (λ et μ). En effet, dans un solide homogène et isotrope, il existe entre les contraintes et les déformations les six relations suivantes :

Les coefficients λ et μ ont les dimensions d’une contrainte (ML^– 1T^– 2).
On a :
Ces relations ont été à la base des études de James Clerk Maxwell (1831-1879). La somme des trois pressions (ou « contraintes ») est proportionnelle à la somme des déformations qu’elles produisent : la différence de leurs pressions est proportionnelle à la différence des déformations en compression qu’elles entraînent.

Équations générales d’équilibre des solides élastiques, homogènes et isotropes

En reprenant les équations (II) et en remplaçant les termes par leur valeur dans le groupe d’équations (IV) ci-dessus, on trouve

ou
avec
En posant X₀ = – X, Y₀ = – Y, Z₀ = – Z,
on obtient finalement :
Ces équations, applicables en tous les points du corps, sont appelées équations indéfinies d’équilibre.

Élasticité plane et photo-élasticité

La théorie de l’élasticité, qui fait appel à la notion d’équilibre interne et à la loi de Hooke, aboutit à des équations différentielles qui ne peuvent être intégrées, en dehors des quelques cas particuliers suivants.

• Compression normale et uniforme. La dilatation cubique θ qui en résulte est égale à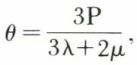

P étant la contrainte en pression.
Le coefficient

est le coefficient de compressibilité.

• Extension longitudinale d’un prisme ou d’un cylindre. Le module d’élasticité longitudinale, ou module d’Young, est égal à

• Équilibre d’une couche cylindrique.

• Cas de la torsion et du cisaillement.

• Problème de Saint-Venant. Il permet de déterminer l’équilibre d’une pièce prismatique ou cylindrique très longue par rapport aux dimensions de sa section transversale et soumise uniquement à des forces appliquées sur les deux bases. Adhémar Barré, comte de Saint-Venant (1797-1886), a ainsi démontré que, dans la section droite d’une pièce prismatique, les efforts normaux se répartissent suivant une fonction linéaire des coordonnées, ouvrant ainsi la porte à toute la résistance des matériaux.

Les méthodes utilisées dans ce domaine simplifient les calculs de la théorie de l’élasticité en faisant intervenir des hypothèses relatives à la fibre moyenne et aux sections normales, mais ne s’appliquent, de ce fait, qu’aux pièces prismatiques longues ; ces calculs demeurent d’ailleurs très complexes pour certains problèmes, et il est impossible d’apprécier l’approximation réalisée par l’adoption d’hypothèses simplificatrices.