Éd. 1971-1976

calcul des prédicats (suite)

Il est tout d’abord possible de former la classe des académiciens : α = df {x|ax}. Cela dit, « les ouvrages des académiciens » seront tout simplement les objets x qui sont ouvrages, non d’un y quelconque, mais d’un membre de α. Ils constitueront donc une nouvelle classe, que nous noterons r‘‘α et qui pourra s’écrire

Comme toutes les classes, les r des α peuvent être vides, même si l’exemple donné ne le laisse pas supposer !

Propriétés du calcul des prédicats

Le calcul des prédicats jouit de diverses propriétés, parmi lesquelles nous retiendrons les suivantes :

• (1) Il est non contradictoire. Cela signifie qu’il n’est pas possible d’y démontrer à la fois un théorème de la forme A et un théorème de la forme Comme le signe est interprété par la négation, on peut encore dire qu’il n’est pas possible d’y démontrer une expression et sa négation ;

• (2) Il est consistant en ce sens qu’il existe au moins une ebf qui n’est pas un théorème.

Remarque. D’une façon générale, on peut montrer qu’un système non contradictoire est nécessairement consistant sans que la réciproque ne soit vraie ;

• (3) Il est complet au sens faible. La signification exacte de cela exige de recourir à la notion de modèle. Intuitivement, la complétude au sens faible signifie que toute ebf qui est vraie dans toutes les interprétations que l’on peut en donner est démontrable dans le calcul ;

• (4) Il n’est pas complet au sens fort. En d’autres termes, il est possible d’ajouter aux schémas d’axiomes du calcul certains schémas d’expressions qui ne sont pas des schémas de théorèmes sans que le système ainsi complété devienne contradictoire. Ainsi, l’adjonction à A₁ — A₅ du schéma

transforme profondément le calcul, mais le nouveau système reste non contradictoire ;

• (5) Il n’est en général pas décidable. Autrement dit, si l’on prend une ebf quelconque A, il n’existe aucune méthode qui permette, en un nombre fini d’étapes, de décider si A est un théorème ou non. En revanche, si A a certaines formes particulières, il peut exister des méthodes de décision. Ce sera par exemple le cas si A ne contient qu’une seule variable X (qui peut être mentionnée un nombre quelconque de fois dans A). On peut donc dire que le calcul des prédicats à une seule variable d’objet est décidable.

J.-B. G.

V. calcul des propositions.

calcul des propositions

Partie de la logique moderne qui étudie les propriétés générales des propositions et des opérateurs propositionnels sans référence au contenu de ces propositions, dont elle ne considère que leur valeur de vérité.

Propositions et tables de vérité

Considérons les propositions grammaticales suivantes :
(1) Homère a écrit « l’Odyssée » ;
(2) L’oxygène est un gaz rare ;
(3) Jules César a été empereur et il est mort aux ides de mars 44 ;
(4) Une baleine n’est pas un poisson ;
(5) Prends un siège Cinna ! ;
(6) Comment allez-vous ?

On voit qu’il y a un sens à se demander si les propositions (1) à (4) sont vraies ou fausses, mais qu’il n’y en a pas à se poser la même question à propos de (5) et (6). Le calcul des propositions ne retient que les propositions susceptibles d’être vraies ou fausses, à l’exclusion, en particulier, des propositions exclamatives et interrogatives. Encore faut-il noter que la détermination de la valeur de vérité d’une proposition donnée n’est pas du ressort de la logique. C’est à la philologie de décider si (1) est vraie, à la chimie de décider si (2) est vraie, et ainsi de suite. La logique se contente ici de prendre en considération des propositions qui peuvent être aussi bien vraies que fausses et dont chacune est soit vraie, soit fausse.

Parmi les propositions retenues, il est encore possible d’en distinguer de deux sortes. Les unes, comme (1) et (2), ne peuvent être décomposées sans perdre leur statut de proposition ou, ce qui revient au même, aucune de leurs parties n’est une proposition : ce sont des propositions atomiques. Les autres peuvent être envisagées comme composées de propositions atomiques : ce sont des propositions moléculaires. Il est ainsi possible de dire que (3) est composée de « Jules César a été empereur », de « il est mort aux ides de mars 44 » à l’aide de l’opérateur de conjonction et. Le cas de (4) est un peu plus délicat. Ce n’est pas une proposition atomique, sens que « Une baleine est un poisson » est encore une proposition (fausse, mais c’en est une). D’autre part, on ne peut pas dire qu’elle soit, à proprement parler, composée. On convient néanmoins de la traiter comme une proposition moléculaire, obtenue par l’application de l’opérateur de négation non : (4) non (une baleine est un poisson).

Le problème qui se pose est alors le suivant : sachant que toute proposition atomique est soit vraie, soit fausse, déterminer la valeur de vérité d’une proposition moléculaire donnée. Cela conduira à déterminer la liste exhaustive des opérateurs qui permettent de composer des propositions entre elles et que nous appellerons des foncteurs propositionnels. Nous allons toutefois commencer par étudier quelques fondeurs particuliers.

Désignons par p une proposition atomique quelconque. Si val (p) signifie « valeur de p » et si 1 désigne le vrai, tandis que 0 désigne le faux, nous savons que val (p) = 1 ou que val (p) = 0. Il est alors conforme à la signification habituelle de non de poser : (*) Si val (p) = 1, alors val (non p) = 0 ; si val (p) = 0, alors val (non p) = 1.

Il est commode d’introduire un signe spécifique pour représenter le foncteur de négation. Nous choisirons le signe Dès lors, l’information contenue dans (*) peut se mettre sous la forme de la table de vérité ci-dessous :

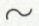Le foncteur de négation porte sur une seule proposition : c’est un foncteur unaire. Le foncteur de conjonction et, quant à lui, relie deux propositions, disons p et q, pour engendrer une troisième proposition. Il s’agit d’un foncteur binaire.

A priori, les propositions atomiques p et q peuvent être chacune vraie ou fausse, indépendamment l’une de l’autre. Cela signifie qu’il faut envisager quatre éventualités :

(1) val (p) = val (q) = 1 ;

(2) val (p)= 1, val (q) = 0 ;

(3) val (p) = 0, val (q)= 1 ;

(4) val (p) = val (q) = 0.