calcul des prédicats (suite)

La relation d’identité

La logique des prédicats qui précède ne contient que des variables. Cela signifie que nous n’y avons fait figurer aucun objet, ni aucune propriété, ni aucune relation spécifiques. Il existe toutefois une relation particulièrement importante, l’identité, que nous allons introduire sous la forme d’une constante notée =

Nous allons la concevoir comme une relation entre variables d’objet, mais, au lieu d’écrire, conformément à nos conventions, = xy pour « x est identique à y », nous noterons selon l’usage x = y.

Ce nouveau signe élargit naturellement le calcul des prédicats, et son usage doit être réglé soit par de nouvelles règles, soit par de nouveaux schémas d’axiomes. En déduction naturelle d’abord, il est possible de poser les deux règles suivantes :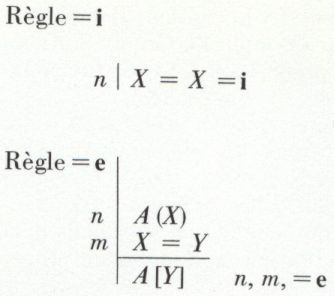

La règle = i se présente comme un schéma d’axiomes. Elle pose que, à tout moment d’une déduction, il est possible d’écrire qu’une variable est identique à elle-même. La règle = e permet de remplacer X par Y dans une expression donnée, à condition que X soit identique à Y.

D’un point de vue axiomatique, les règles R₁ et R₂ suffisent à condition de poser les deux schémas suivants, qui sont d’ailleurs entièrement équivalents aux règles = i et = e :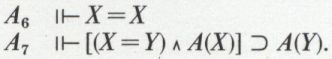

Il est facile de démontrer les théorèmes suivants :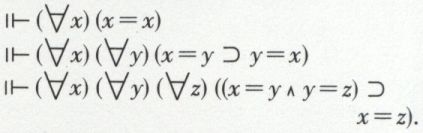

On voit que la relation d’identité est totalement réflexive, qu’elle est symétrique et transitive. C’est donc une relation d’équivalence. (V. classes et relations.)

Remarques.

1. Si nous disposions d’un calcul des prédicats du deuxième ordre, nous pourrions introduire la relation d’identité par une simple définition :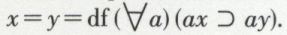

2. Le point de vue extensionnel reparaît ici sous l’espèce de la règle = e et du schéma d’axiomes A₇. Il existe en effet des contextes, dits intensionnels, dans lesquels il n’est pas possible de remplacer une expression par une autre qui lui est identique. En voici un exemple : « Soit n le nombre des enfants de Paul. Jean ne sait pas que n > 3. Or n = 5. Donc (par remplacement) Jean ne sait pas que 5 > 3 ».

Quelques définitions

Il est possible, sans élargir le calcul, d’y introduire toutes sortes de notions utiles et cela par simples définitions. En voici quelques-unes.

• (1) Un et un seul. 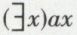est interprété par « il existe au moins un x tel que ax ». Pour spécifier que x est unique, il suffit d’ajouter que tout autre objet qui jouirait de la propriété a serait identique à x. On posera donc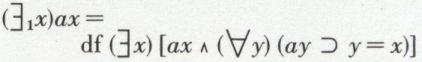

et on lira 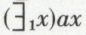 : « il existe un seul x tel que ax ».

(2) Le ... de. Soit l’expression « le satellite naturel de la Terre ». Elle désigne la Lune, mais elle ne peut le faire que parce que deux conditions sont satisfaites :
(1) La Terre a un satellite naturel ;
(2) Elle n’en a qu’un.

En conséquence, des expressions comme « le satellite de Mercure » ou « le satellite de Jupiter » doivent être considérées non comme fausses, ce qui n’aurait aucun sens puisque seule une proposition peut être fausse, mais comme dépourvues de signification.

Posons donc ax = df x est satellite naturel de la Terre. Puisque l’on a 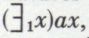il y aura un sens à introduire la notation 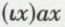pour signifier « le x tel que x est satellite de la Terre ».

Plus généralement, et à la condition que 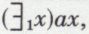l’expression 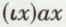représente la description d’un élément de l’univers du discours. Il s’agit donc là d’un procédé propre à suppléer l’absence de constantes d’objet dans le calcul des prédicats. En effet, supposons que l’on veuille exprimer dans le système la proposition « la Lune brille ». On commencera par transformer la proposition donnée en « le satellite naturel de la Terre brille » et, si l’on pose bx = df x brille, on écrira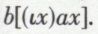

Remarques.
1. Le descripteur 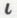est un opérateur qui lie la variable sur laquelle il porte. On pourra donc écrire plus simplement 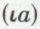au lieu de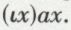
2. Il n’est possible d’introduire l’opérateur 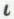que de façon contextuelle. On pourrait poser par exemple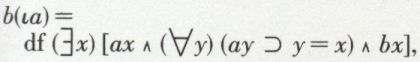

encore que ce ne soit pas la façon la plus simple de procéder.

Passons maintenant à un exemple où la description fait usage d’une relation r et non plus d’une propriété a. Supposons, pour fixer les idées, que rxy signifie « x est le sinus de y ». Puisque, quel que soit le nombre réel y, il lui correspond un et un seul nombre qui est la valeur de son sinus, il sera légitime d’écrire 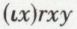pour désigner « le sinus de y ». On posera sous les conditions d’existence et d’unicité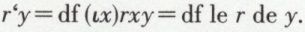

• (3) Les ... de. Supposons que rxy = df x est enfant de y et que le y auquel on a affaire ait en réalité plusieurs enfants. Dans ces conditions, « les enfants de y » constituent une classe, à savoir { x | rxy } (v. classes et relations). Posons alors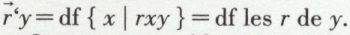

On voit que, s’il se trouvait que y n’ait qu’un enfant, la classe r‘y se réduirait à un seul élément. L’expression devrait se lire « l’enfant de y », mais la définition resterait correcte. Enfin, grâce à la classe vide, elle le resterait même si y n’avait pas d’enfant. (Il est cependant clair qu’il faut être logicien pour dire encore « les enfants de y » sous-entendant « constituent la classe vide ».)

Remarque. Même si 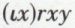et r‘y peuvent toutes deux se lire « le r de y » dans le cas où x est unique, elles correspondent toutefois à deux notions bien distinctes. Supposons que x₁ soit le r en question. Alors :
représente l’objet x₁ et 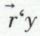représente la classe qui contient x₁, soit {x₁}.

D’une façon analogue, on introduira la notation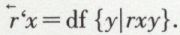

La différence est la suivante : r‘y désigne les antécédents de la relation r, et r‘x les conséquents. Ainsi, si rxy = df x est enfant de y, r‘y désigne « les enfants de y » et r‘x désigne « les parents de x ».

• (4) Les ... des. Si l’on analyse une expression comme « les ouvrages des académiciens », on constate qu’elle fait appel à une relation et à une propriété. Posons
rxy = df x est ouvrage de y
et ax = df x est académicien.