Caractéristiques de la loi binomiale

Espérance mathématique

L’espérance mathématique de la variable de Bernoulli ℬ (1, p) est E [ℬ (1, p)] = 0 × q + 1 × p = p.
Comme la variable binomiale ℬ (n, p) est la somme de n variables de Bernoulli, son espérance est

Le calcul direct donne d’ailleurs

puisque p + q = 1.

Variance

La variance de la variable de Bernoulli ℬ (1, p) est
V [ℬ (1, p)] = q (0 – p)² + p (1 – p)² = qp² + pq² = pq (p + q) = pq.
Comme la variable binomiale ℬ (n, p) est la somme de n variables de Bernoulli indépendantes, sa variance est

Son écart type est donc

Exemple. Au jeu de pile ou face en quatre coups 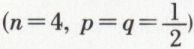, X étant le nombre de piles obtenues, l’espérance et la variance sont

d’où σ = 1 ; on peut espérer deux succès avec un écart type de 1.

Loi des grands nombres

Si X₁, X₂, ..., X_n sont des variables aléatoires indépendantes et de même loi, la variable aléatoire est telle que, pour tout nombre réel ε > 0, la probabilité tend vers zéro lorsque n augmente indéfiniment, E (X_i) étant l’espérance mathématique commune aux variables X₁, X₂, ..., X_n. Appliquée à une variable binomiale, elle prend une forme particulière.

La variable binomiale X = ℬ (n, p) est en effet la somme de n variables de Bernoulli, ℬ_i (1, p) = X_i indépendantes, de même loi et d’espérance E (X_i) = p. La variable , que l’on peut interpréter comme le rapport du nombre de succès au nombre d’épreuves, c’est-à-dire la fréquence du succès, est donc telle que

quand n → + ∞. Ainsi, on est presque sûr qu’en répétant indéfiniment la même épreuve la fréquence va se rapprocher de la probabilité p de succès.

De façon précise, l’espérance mathématique et la variance de la variable sont respectivement et  ; l’inégalité de Bienaymé-Tchébychev appliquée à la variable s’écrit alors

La quantité ε étant > 0, on pourra choisir n de façon à rendre plus petit qu’une quantité fixée à l’avance.

Exemple. Au jeu de pile ou face, on cherche la valeur minimale du nombre de coups nécessaires à l’obtention d’une fréquence de succès (pile par exemple) comprise entre 0,45 et 0,55, avec une probabilité de 0,99. Il faut, pour cela, que

ce qui sera réalisé si , soit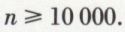

Approximations de la loi binomiale

Par une loi de Poisson

Quand n est grand (par exemple, ), p petit (par exemple, 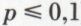) et quand le produit np est de l’ordre de quelques unités (par exemple, np < 5), on peut remplacer, avec une assez bonne précision, la valeur numérique de b (k, n, p) par celle de , avec m = np. Le calcul de P (k, m) est moins pénible que celui de b (k, n, p). D’ailleurs, la table de la loi de Poisson donnant les valeurs de P (k, m) est moins volumineuse que la table binomiale, car P (k, m) ne dépend que d’un paramètre, m, pour une valeur de k donnée, alors que b (k, n, p) dépend de deux paramètres, n et p.

Par une loi de Laplace-Gauss

Si n est grand (par exemple, 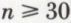), quand p n’est ni trop petit, ni trop grand, de façon que les produits np et nq soient supérieurs à quelques unités (par exemple, np > 5 et nq > 5), on peut remplacer la valeur numérique de b (k, n, p) par celle de
Malgré les apparences, la formule donnant P (k) conduit à un calcul bien plus simple que celui de b (k, n, p), où figurent des factorielles, car

D’ailleurs, la table de la loi de Laplace-Gauss fournit la valeur de

Il suffit donc de calculer
de chercher f(t) dans la table de la loi de Laplace-Gauss et de diviser par puisque
On peut aussi, dans les mêmes conditions calculer des probabilités cumulées relatives à la loi binomiale ℬ (n, p) à l’aide de la fonction de répartition F (t) de la loi de Laplace-Gauss. On peut, pour cela, remplacer

La table de la loi de Laplace-Gauss donne les valeurs de

Il suffit donc de calculer t₁ et t₂, et de remplacer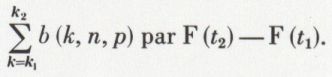

E. S.

➙ Aléatoire (variable) / Gauss (C.) / Poisson (D.) / Probabilité.

 G. Calot, Cours de statistique descriptive (Dunod, 1964). / Y. Hébert, Mathématiques, probabilités et statistique (Vuibert, 1975).