Binet (Alfred) (suite)
Ce test mental s’adresse à l’intelligence considérée comme une aptitude globale innée ; pour cela sont écartées soigneusement les épreuves pouvant faire appel à un quelconque apprentissage (comme les connaissances scolaires) et que les individus possèdent à des degrés divers. Il est composé d’épreuves de difficultés croissantes groupées par âges successifs de trois ans à treize ans. Une épreuve est caractéristique d’un âge donné si elle est réussie par la moyenne des enfants de cet âge. L’intelligence se trouve ainsi définie opérationnellement : c’est le niveau auquel se situe un individu par rapport à son groupe d’âge, ce qui permet à Binet de proposer une unité, l’âge mental. On dit qu’un enfant de cinq ans a un niveau intellectuel normal s’il a cinq ans d’âge mental, c’est-à-dire s’il a réussi toutes les épreuves de cinq ans et aucune d’un niveau supérieur. Si ce même enfant ne peut réussir que les épreuves de quatre ans, son âge mental est de quatre ans et il présente un retard intellectuel.
L’idée d’une mesure de l’intelligence se trouvait déjà chez Francis Galton (1889), mais celui-ci pensait que l’on pouvait l’appréhender à travers ses manifestations les plus simples, comme la discrimination sensorielle ; Binet préfère une appréhension directe, même élémentaire des processus supérieurs ; il utilise une multitude d’épreuves permettant d’envisager toute l’étendue du champ de l’intelligence.
La valeur diagnostique du test de Binet et Simon est vérifiée par la bonne corrélation entre le résultat d’un enfant au test et le jugement de l’instituteur sur cet enfant. Cette échelle, remaniée par Binet sur des points de détail en 1908 et 1911, a tout de suite connu un grand succès en France, mais également en Angleterre et aux États-Unis, où Lewis M. Terman en a fait de nombreuses adaptations. En France, l’adaptation la plus récente est celle de René Zazzo (1968), et, sous cette forme, le test de Binet et Simon est encore largement utilisé, ce qui montre l’intérêt historique et aussi actuel de l’œuvre de Binet.
A. D.
➙ Intelligence / Sensation / Tests mentaux.
F. Zuza, Alfred Binet et la pédagogie expérimentale (Vrin, 1948). / M. Reuchlin, Histoire de la psychologie (P. U. F., coll. « Que sais-je ? », 1957 ; 8e éd., 1972). / Revue de psychologie appliquée (numéro spécial, t. VII, 1957). / G. Avanzini, la Contribution de Binet à l’élaboration d’une pédagogie scientifique (Vrin, 1969).






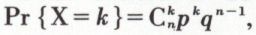 p étant un nombre compris entre 0 et 1 et q = 1 – p.
p étant un nombre compris entre 0 et 1 et q = 1 – p.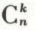 , noté aussi
, noté aussi 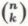 , est donné par
, est donné par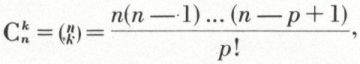
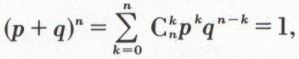
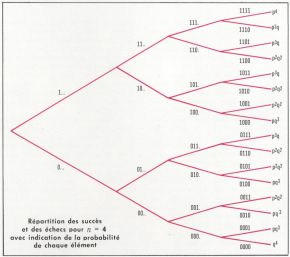
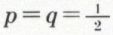 et n = 3 ; on obtient la loi de probabilité suivante :
et n = 3 ; on obtient la loi de probabilité suivante :
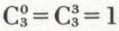 ,
, 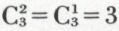 et
et 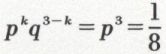 . Cette loi particulière est celle de la variable aléatoire X égale, par exemple, au nombre de piles amenées par une pièce de monnaie au jeu de pile ou face en trois coups.
. Cette loi particulière est celle de la variable aléatoire X égale, par exemple, au nombre de piles amenées par une pièce de monnaie au jeu de pile ou face en trois coups.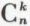 façons différentes parmi les n épreuves successives, car chaque répartition correspond à une partie à k éléments prise dans un ensemble à n éléments, et le nombre de ces parties est
façons différentes parmi les n épreuves successives, car chaque répartition correspond à une partie à k éléments prise dans un ensemble à n éléments, et le nombre de ces parties est  . Les événements correspondant aux
. Les événements correspondant aux 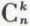 répartitions ayant tous la même probabilité, pkqn–k, la probabilité de k succès en n épreuves est donc égale à
répartitions ayant tous la même probabilité, pkqn–k, la probabilité de k succès en n épreuves est donc égale à 

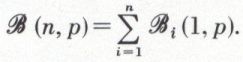

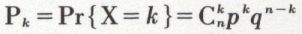 n’est en général pas aisé. On calcule de proche en proche, en utilisant le rapport
n’est en général pas aisé. On calcule de proche en proche, en utilisant le rapport 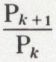 , les différentes valeurs de Pk. Ce rapport a pour valeur
, les différentes valeurs de Pk. Ce rapport a pour valeur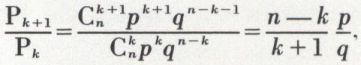
 et
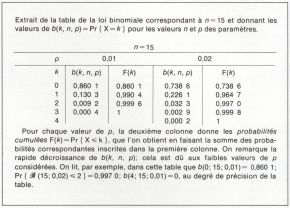
et 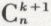 en fonction de n et de k. On peut alors construire des tables de la loi binomiale, pour différentes valeurs de n et p, avec
en fonction de n et de k. On peut alors construire des tables de la loi binomiale, pour différentes valeurs de n et p, avec