Russell (Bertrand) (suite)

Parmi les œuvres de Russell, il faut encore citer : Mysticism and Logic, and Other Philosophical Essays (1918), The France and Theory of Bolchevism (1920), The Problems of China (1922), On Education (1926), The Analysis of Matter (1927), An Outline of Philosophy (1927), Marriage and Morals (1929), The Conquest of Happiness (1930), Education and the Social Order (1932), Power : a New Social Analysis (1938), Human Society in Ethics and Politics (1954).

La logique et la philosophie de Russell

Les fonctions propositionnelles

La logique à laquelle Russell croit possible de réduire les mathématiques (logicisme) comprend le calcul* des propositions et le calcul* des prédicats avec variables de prédicat quantifiées. Le nom de fonction propositionnelle, dont il emprunte à G. Frege l’idée, recouvre plusieurs conceptions.
a) La fonction propositionnelle comme énoncé ouvert. Un exemple en est « x est mortel », issu de la proposition « Socrate est mortel » quand on remplace le nom propre « Socrate » par une variable d’individu. En tant qu’énoncé ouvert, une fonction propositionnelle désigne une valeur de vérité ambiguë (elle n’est ni vraie ni fausse). Elle ne devient le nom d’une valeur de vérité qu’une fois que la ou les variables libres qui y figurent sont remplacées par des noms d’objets déterminés, « x est mortel » est vrai de Socrate, faux d’un objet éternel, par exemple pour « 2 » substitué à x.
b) La fonction propositionnelle comme prédicat avec variables en forme nominale. Ainsi, l’écriture φ xyz, si x, y et z ne sont pas considérés comme des variables libres, mais comme des marqueurs de place destinés à montrer de combien d’arguments dépend φ, est un prédicat dans ce sens. L’équivoque des variables libres est que celles-ci peuvent jouer plusieurs rôles différents.
c) La fonction propositionnelle comme fonction logique, c’est-à-dire comme application d’un domaine d’individus (ou d’un domaine de n-uples d’individus) dans l’ensemble des valeurs de vérité : il s’agit alors non plus, comme dans a et b ci-dessus, d’un objet linguistique, mais d’un objet abstrait susceptible d’interpréter une fonction propositionnelle comme entité linguistique.
d) La fonction propositionnelle en tant qu’abstract ou en tant qu’attribut (ou nom d’attribut). Lorsqu’on assigne des fonctions logiques aux fonctions propositionnelles, on adopte un principe d’extensionnalité : des fonctions logiques sont équivalentes exactement si elles sont vraies des mêmes objets. (En extension, une fonction logique est une classe.) Ce principe ne peut s’appliquer aux attributs sans les réduire aux classes. Russell semble hésiter à donner aux abstracts, c’est-à-dire aux expressions telles que 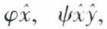etc., le statut (de noms) d’attributs ou celui (de noms) de classes. 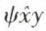peut se lire : le fait d’entretenir avec y la relation ψ.

L’implication formelle

La notion de fonction propositionnelle combinée à celle d’implication (⊃) permet de définir l’implication formelle. φ et ψ étant des fonctions propositionnelles à une place, φx ⊃ _xψx est une implication formelle, caractérisée par la récurrence, dans l’antécédent et dans le conséquent, de la même lettre liée par un quanteur portant sur toute l’expression.

Russell ne se borne pas à considérer les fonctions propositionnelles qui résultent d’une proposition par substitution de variables aux noms propres ou aux constantes, qui sont des valeurs particulières de leurs arguments (par exemple, de la substitution de x à a dans φa). Il considère aussi les fonctions propositionnelles qui résultent de ce qu’on fait varier φ : ainsi, on passe de φ(Socrate) à ψ(Socrate) ou à ∃φφ(Socrate). Cette possibilité avait déjà été étudiée par Frege.

Les classes

Russell a eu plusieurs conceptions des classes. L’une d’elles est la théorie zigzag (1903 et 1906) : seules déterminent une classe les fonctions propositionnelles suffisamment simples. L’étude des paradoxes qui rendaient suspecte la notion de classe conduisit Russell à préférer une théorie « pas de classes », qui consiste à soutenir qu’on peut se servir de symboles de classe sans avoir pour autant à reconnaître l’existence des classes : la notion de classe représente une simple manière de parler, et les symboles de classe sont des abréviations. Il faut alors donner des règles permettant de traduire les expressions qui contiennent de tels symboles en d’autres expressions qui n’en contiennent plus. C’est une entreprise de réduction nominaliste. Techniquement, la réduction s’effectue au moyen de définitions contextuelles. Les classes s’introduisent sans qu’on ait besoin d’une notion nouvelle, « les x tels que φx » s’écrivant « {x : φx} », et « y ∈ {x : φx} » équivaut à « φy ». Sur la base de cette définition contextuelle, on peut développer l’algèbre booléienne des classes et (à partir d’une définition analogue) celle des relations. L’existence de ces objets est simulée (Quine), puisque φy peut partout remplacer y ∈ {x : φx} (chaque fois qu’on parle de la classe, on parle, en fait, des valeurs de vérité d’une fonction propositionnelle). Mais ce procédé devient inutilisable quand interviennent des classes de classes, qui sont nécessaires en théorie des nombres cardinaux. L’expression
{x : φx} ∈ α ≡ ∃β [∀y(y ∈ β ≡ φy) & β ∈ α],
qui permet d’éliminer l’abstract de classe {x : φx}, contient, en effet, des variables de classes liées.

La théorie des types

Les types peuvent être considérés comme des collections d’objets susceptibles d’être membres d’un même objet. Le type le plus bas sera constitué par les individus ; ensuite vient le type des classes dont les éléments sont des individus ; puis vient le type des classes de classes ; et ainsi de suite. Pour les relations binaires entre individus (classes de paires ordonnées), on aurait des types à deux dimensions, etc.

Par rapport au symbolisme logique, les types sont des domaines d’entités où les variables des différentes espèces (variables d’individu, de fonction propositionnelle d’individus, etc.) prennent leurs valeurs. Ce sont les « range of significance » des fonctions propositionnelles, c’est-à-dire les ensembles d’objets pour lesquels les valeurs de ces fonctions propositionnelles sont définies (autrement dit, les valeurs pour lesquelles ces fonctions sont vraies ou fausses). De plus, si x et y sont des expressions désignant des objets du même type, la substitution de y à x dans n’importe quel contexte changera éventuellement la valeur de vérité de ce contexte ; elle ne transformera pas une expression douée d’une valeur de vérité en une autre qui n’en a pas.