Russell (Bertrand) (suite)

Par ailleurs, Russell traitait aussi les types comme des collections d’expressions ou comme des notations associées aux expressions. Une telle conception relève de la linguistique et non plus de l’ontologie. Ainsi, on parle parfois du type d’une expression ou d’attacher des indices de type aux expressions. Lorsqu’on a affaire au type d’une proposition (qui dépend du type des fonctions propositionnelles qui y figurent), le type est plutôt conçu comme une notation que comme un objet. Russell remarquait lui-même que la théorie des types est en fait une théorie des symboles plutôt que des entités (et, en effet, son propos est de définir les expressions bien formées).

Cette théorie des types fut suggérée à Russell par l’étude du paradoxe très élémentaire qui porte son nom, à savoir celui de la classe de toutes les classes qui ne sont pas éléments d’elles-mêmes. Pour empêcher la contradiction, Russell pose que x ∈ x et x ∉ x sont mal formés. D’une façon générale, l’expression figurant à gauche de ∈ doit être du type immédiatement inférieur à celui de l’expression qui apparaît à sa droite.

Étant donné la manière progressive dont se construisent les types, on n’a jamais C_α ∈ C_α pour un type α. Cette exclusion est la conséquence du principe du cercle vicieux (en abrégé PCV) sous la forme suivante : « Tout ce qui suppose la totalité d’une collection ne peut être un élément de cette collection » (en admettant qu’une collection se suppose elle-même) ; mais la théorie des types s’appuie sur des considérations de catégories sémantiques et de substitution qui préservent la correction grammaticale ; elle n’implique pas le PCV. Celui-ci a des conséquences plus fortes que l’exclusion des paradoxes triviaux. Une de ses versions dit qu’aucune totalité ne doit contenir comme éléments des objets qui ne sont définissables qu’en termes de cette totalité ou, plus précisément encore, « tout ce qui contient une variable apparente (= liée) ne doit pas être une valeur possible de cette variable » (1906, p. 634). Cela exclut ce qu’on appelle depuis lors, d’après Poincaré et Russell, les définitions imprédicatives. Ces définitions se caractérisent par le fait qu’un quanteur figurant dans le definiens parcourt un ensemble auquel appartient l’objet défini. On aura une définition de ce genre si l’on introduit un ensemble de nombres naturels par une ; expression renfermant un quanteur portant sur tous les ensembles de nombres naturels (tous inclut le nouvel ensemble qu’on est en train de définir).

Le PCV a pour conséquence qu’une collection d’ensembles ne doit pas être traitée comme achevée ; autrement dit, elle ne sera pas un domaine de valeurs pour une variable quantifiée.

On a appelé (Chwistek, Ramsey) théorie simple des types la hiérarchie des types indiquée ci-dessus et théorie ramifiée des types celle qui est conforme au PCV dans sa deuxième et sa troisième version : les définitions imprédicatives proscrites par le PCV ne sont pas en infraction avec la hiérarchie des types simples. La théorie ramifiée empêche aussi bien les paradoxes sémantiques ou épistémologiques que les paradoxes logiques.

Dans la théorie ramifiée, un ordre est attaché aux notations ou aux objets qui leur correspondent. Une fonction propositionnelle qui dépend d’une variable d’individu et qui devient une proposition par substitution à cette variable d’un nom d’individu est dite fonction du premier ordre (définition analogue pour le cas de plusieurs variables d’individu). Une fonction propositionnelle qui contient une variable de fonction liée par un quanteur ou par l’abstracteur sera dite fonction du second ordre. Par exemple, la fonction qui peut se lire « avoir toutes les propriétés de y », est d’ordre deux si φ est d’ordre un ; la fonction propositionnelle « être vrai d’exactement tous les objets qui vérifient ψ », dépend d’une variable φ liée par l’opérateur d’abstraction. Si φ est d’ordre un, est d’ordre deux, et l’expression totale est d’ordre deux ; si, en outre, ψ est d’ordre un, l’expression totale est une fonction prédicative, c’est-à-dire que son ordre est supérieur d’une unité à celui de son argument ψ ; sous forme non explicite, elle peut s’écrire f!(ψ!x), le point d’exclamation indiquant la prédicativité (une fonction du premier ordre est automatiquement prédicative). 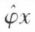Un autre exemple de fonction prédicative est la fonction propositionnelle déjà mentionnée, « avoir même extension que ψ », qui est prédicative lorsque et sont d’ordre un, étant alors d’ordre deux.

Au contraire, la fonction propositionnelle « avoir toutes les propriétés d’un grand général », qui se paraphraserait par
n’est pas du même ordre que « est un grand général », qui est une fonction d’individu, donc du premier ordre ; elle emporte une référence à toutes les fonctions propositionnelles 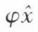du premier ordre ; elle est du second ordre et n’est pas prédicative.

La théorie ramifiée des types a pour conséquence qu’on n’a jamais plus à rencontrer ni à utiliser la notion d’ensemble quelconque. On n’aura affaire qu’à des ensembles définis par des conditions d’un certain ordre, et cela pour chaque type (les exemples qui précèdent n’ont mis en jeu que deux types : celui des individus et celui des classes d’individus ; bien entendu, le type des individus ne se ramifie pas). Une des conséquences particulières de la théorie ramifiée est que deux fonctions propositionnelles peuvent déterminer des classes identiques (c’est-à-dire les mêmes objets les vérifient, et tout objet qui est dans une de ces classes est aussi dans l’autre, et réciproquement), tout en étant d’ordre différent et donc distinctes. Cela montrerait que Russell est passé de la considération des classes et des relations à celle des attributs avec abandon de l’extensionnalité (ses fonctions propositionnelles sont implicitement devenues des [noms d’] attributs, point sur lequel a insisté Quine).