Éd. 1971-1976

résonance électrique (suite)

Avec un courant de fréquence industrielle, il est difficile d’avoir un facteur de surtension important sans employer des bobines à noyau de fer doux ; mais, pour des courants de haute fréquence, on arrive facilement à des valeurs de plusieurs centaines. Ainsi, pour la fréquence N = 10⁶ Hz = 1 MHz, on obtient un circuit résonnant ayant un facteur de qualité Q = 100 en branchant en série une bobine d’induction 1,6 μH, de résistance 0,1 Ω, et un condensateur de capacité 16 . 10^–3 μF.

Bande passante

Lorsque le facteur de qualité a une valeur élevée, la résonance est aiguë ; si l’on applique entre les bornes de la portion de circuit une différence de potentiel de valeur efficace constante mais dont la pulsation prend différentes valeurs, l’intensité varie. On appelle courbe de résonance le graphe obtenu en portant les valeurs de l’intensité du courant en fonction de sa fréquence N. Lorsque la résonance est aiguë, cette courbe présente un pic pour N = N₀, fréquence de résonance ou fréquence propre du circuit ; elle montre que l’intensité n’est notable que si la fréquence imposée est suffisamment voisine de la fréquence de résonance. Pratiquement, le circuit ne laisse passer le courant que dans une bande de fréquences entourant N₀, bande dont la largeur diminue quand l’acuité de la résonance croît. Pour un circuit de résistance R, dont l’impédance à la résonance vaut donc R, on admet que cette bande de fréquence, appelée bande passante, comprend toutes les fréquences pour lesquelles l’impédance est inférieure à . La largeur ΔN de cette bande est telle que :

Les choses se compliquent lorsque l’on considère un circuit de forte résistance, où l’amortissement est important ; le pic de la courbe de résonance, très aplati, n’a plus lieu pour une fréquence égale à la fréquence propre N₀, mais pour une fréquence plus élevée : on dit que la résonance est floue. Le pic de résonance peut même disparaître.

Résonance parallèle circuit bouchon

Lorsqu’une portion de circuit est constituée par une bobine d’inductance L et de résistance négligeable, en parallèle avec un condensateur de capacité C, son impédance prend la valeur :

Dans le cas où L, C et ω vérifient la relation LCω² = 1, correspondant à la résonance, l’impédance du circuit devient infinie, l’intensité du courant total est nulle. On peut dire que ce circuit s’oppose au passage du courant, d’où son nom de circuit bouchon. Il est important de remarquer que, si le courant total est nul, cela ne veut pas dire qu’aucun courant ne traverse la bobine ni le condensateur ; en réalité, ces courants existent et peuvent même être très intenses, mais leurs valeurs instantanées sont égales et de sens contraires à chaque instant, si bien que le courant total, qui est leur somme, est constamment nul. En pratique, la bobine, au moins, a une certaine résistance, et l’impédance à la résonance vaut :

elle est très grande si R est très petit devant Lω.

A. T.

résonance magnétique

Phénomène d’interaction qui peut se produire entre une onde hertzienne (onde de radio, de télévision ou de radar) et un atome (un ion ou une molécule) lorsque ce dernier est également soumis à un champ magnétique constant.

Ce phénomène se produit seulement lorsque la fréquence de l’onde a une valeur bien précise proportionnelle au champ magnétique.

Les expériences de résonance magnétique constituent un des plus puissants moyens d’investigation dont disposent les physiciens qui étudient la structure de la matière. Elles ont aussi de nombreuses applications pratiques ; la plus répandue est la construction de magnétomètres de haute précision, permettant en particulier la mesure des champs magnétiques très faibles.

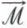Le phénomène de résonance magnétique se produit seulement avec les systèmes atomiques qui possèdent un vecteur moment magnétique . On sait que le moment magnétique d’un petit circuit électrique est défini à partir du mouvement de rotation des charges électriques à l’intérieur du fil conducteur qui constitue le circuit ; il est dirigé suivant l’axe du mouvement de rotation. De la même façon, l’ensemble des mouvements de rotation des électrons* à l’intérieur d’un atome lui confèrent un moment magnétique.

Mais les électrons internes de l’atome ne sont pas seulement porteurs d’une charge électrique q ; ils ont aussi une masse m. Et, pour décrire les mouvements de rotation des points matériels massiques, la mécanique utilise la notion de vecteur moment cinétique (produit vectoriel du rayon vecteur avec la vitesse multipliée par la masse m).

Les mouvements de rotation des électrons donnent donc à l’atome simultanément du moment magnétique et du moment cinétique. On obtient son moment magnétique global et son moment cinétique global en faisant la somme des contributions individuelles des électrons. On peut alors montrer que les vecteurs résultants et sont parallèles entre eux ; ce qui permet d’écrire :

La quantité γ qui figure dans cette équation s’appelle le rapport gyromagnétique de l’atome ; elle varie d’un atome à l’autre ; pour un atome donné, elle peut encore dépendre de l’état dans lequel il se trouve. La notion de rapport gyromagnétique peut être vérifiée en pratique par diverses expériences dont les plus importantes sont celles de résonance magnétique. Mais, à partir de cette même notion fondamentale, on peut donner deux explications assez différentes de la résonance magnétique.

La première explication reste dans le cadre de la mécanique classique ; l’atome, ayant un moment cinétique , se comporte comme une toupie en rotation autour de son axe, mais une toupie dont l’axe porterait un aimant permanent de moment . Sous l’action du champ magnétique , l’axe de la toupie est donc soumis à un couple proportionnel à la fois à ℳ et à B₀ ; le problème posé est analogue à celui d’un gyroscope ; et on montre alors que l’axe de la toupie est soumis au mouvement de précession de Larmor : rotation autour du champ avec la vitesse angulaire ω₀ = γ B₀, appelée vitesse de Larmor.