puissance

MATHÉMATIQUES

Fonction puissance

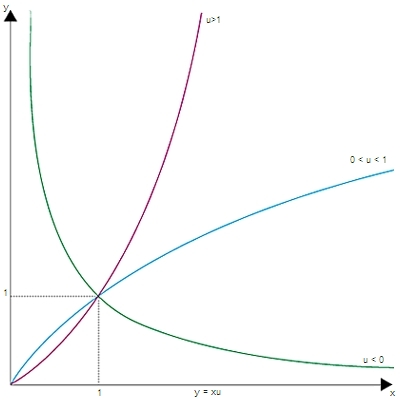
La fonction puissance est une application définie de ℝ^+* dans ℝ^+* qui, un réel u quelconque étant choisi, à tout réel x associe le réel x^u (se lit « x exposant u ») défini par x^u = e^{u ln x}.

u étant un réel quelconque, si l'on note P_u la fonction puissance qui à x > 0 associe le réel positif x^u, on a pour tout couple x, y de réels positifs non nuls :

P_u (x, y) = P_u (x) P_u (y).

P_u est donc un homomorphisme du groupe multiplicatif ℝ^+* dans lui-même ; si u ≠ 0, c'est un isomorphisme (l'isomorphisme réciproque est alors P_1/u). Pour u > 0, P_u est strictement croissante et se prolonge par continuité pour x = 0 en posant P_u (x) = 0. Pour u < 0, P_u est strictement décroissante. (Voir figure.)

Puissance d'un réel x

Si u ∈ ℤ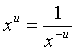^−*, (x ≠ 0).
Si u ∈ ℚ^* et x ∈ ℝ^+*, x^u = x^p/q = (x^1/q)^p, où x^1/q est le réel positif α, encore noté 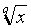tel que α^q = x et p/q un représentant quelconque de u ;
0^u = 0 si u ∈ ℚ^+* ;
x⁰ = 1 si x ∈ ℝ^+*.
Si u ∈ ℝ et x ∈ ℝ^+*, x^u = e^{u ln x}.
Quels que soient les exposants u et v, les calculs sur les puissances se font à l'aide des propriétés suivantes :
― x^u × x^v = x^u+v ;
― x^u × y^u = (x × y)^u ;
― (x^u)^v = x^uv, x et y satisfaisant les conditions requises.