mécanique analytique (suite)

• Théorème de la quantité de mouvement. La variation géométrique par unité de temps de la quantité de mouvement d’un système de masses est égale à la somme géométrique des forces extérieures. La variation géométrique par unité de temps du moment cinétique est égale à la somme géométrique des moments des forces extérieures par rapport à un point fixe. Ce théorème s’énonce plus souvent sous sa forme analytique : La variation algébrique par unité de temps de la composante du moment cinétique ou moment de la quantité de mouvement par rapport à un axe est égale à la somme du moment des forces par rapport à cet axe.

Principe des travaux virtuels

La dynamique repose tout entière sur le postulat suivant : à chaque instant, toutes les forces appliquées à chaque élément de masse d’un corps, y compris la force fictive d’inertie, se font équilibre. On appelle déplacement virtuel d’un point un déplacement imaginé sans s’inquiéter de savoir s’il se produit réellement. Le travail virtuel d’une force est le travail de cette force pour un déplacement virtuel de son point d’application. Toute la statique des systèmes à liaisons bilatérales et sans frottement se résume dans l’énoncé suivant : La condition nécessaire et suffisante pour qu’un tel système soit en équilibre est que la somme des travaux des forces directement appliquées à ce système soit nulle pour tout ensemble de déplacements virtuels compatible avec les liaisons.

Ce théorème du travail virtuel a d’ailleurs un corollaire important : Quand un système est en équilibre, on peut, sans troubler cet équilibre, introduire telle liaison que l’on veut.

On passe du théorème des travaux virtuels en statique à son application à la dynamique des systèmes en lui appliquant le principe de d’Alembert. Le mouvement a lieu de telle façon qu’il y ait à chaque instant équilibre en vertu des liaisons entre les forces appliquées et les forces d’inertie. Par conséquent, la somme des travaux des forces données et des forces d’inertie est nulle à chaque instant pour tout ensemble de déplacements compatible avec les liaisons.

Comme en statique, quand le système est en équilibre, on peut, sans troubler cet équilibre, introduire telles nouvelles liaisons que l’on veut. Les forces données, les forces de liaison extérieures et les forces d’inertie forment un système de vecteurs équivalent à zéro, c’est-à-dire que leur résultante de translation est nulle ainsi que leur moment résultant par rapport à tous points de l’espace. Enfin, tous les théorèmes de la statique étant des conséquences du théorème du travail virtuel (car il revient au même d’utiliser la règle du parallélogramme ou du funiculaire des forces que d’utiliser le principe du travail virtuel), ces théorèmes subsistent intégralement et en totalité en dynamique, pourvu que l’on tienne compte des forces d’inertie.

Mais il faut bien définir le cadre dans lequel le principe des travaux virtuels s’applique, en soulignant les conditions essentielles. Dans la situation actuelle du système, le travail de toutes les forces, y compris celles d’inertie, est nul pour tous les déplacements compatibles avec les liaisons telles qu‘elles existent actuellement. Il s’agit non de déterminer le travail effectif des forces dans les déplacements, mais d’écrire que ces forces se font actuellement équilibre.

Expression analytique du principe du travail virtuel

En coordonnées cartésiennes, il s’écrit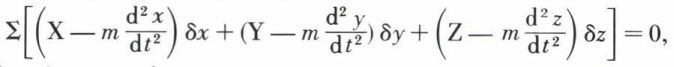

ou, ce qui revient au même :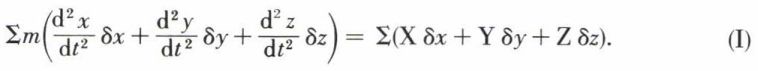

Les quantités δx, δy et δz sont les déplacements virtuels compatibles avec les liaisons au temps t. Ils diffèrent généralement des déplacements réels. Si
φ₁ = 0, φ₂ = 0, ..., φ_p = 0
sont les p conditions auxquelles sont assujetties les n points du système, celles-ci peuvent contenir le temps explicitement, ce qu’on exprime en disant que les liaisons dépendent du temps.
Les quantités dx₁, dy₁, dz₁, ... satisfont aux équations

Quant aux déplacements virtuels δx₁, δy₁, δz₁, ils satisfont aux équations

L’équation (I) ci-dessus a la même forme que celle qui donne l’expression analytique du théorème des forces vives. En effet, si l’on reprend les équations fondamentales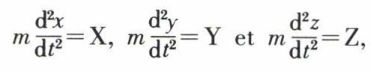

et que l’on multiplie la première par dx, la seconde par dy, la troisième par dz en additionnant et en faisant la somme pour toutes les masses dont se compose le système, on trouve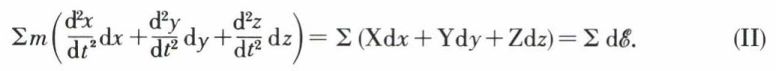

Cette dernière équation a la même forme que l’équation (I).

Si v est la vitesse de la masse m, on a :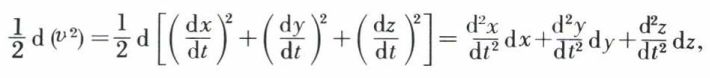

et l’équation (II) s’écrit :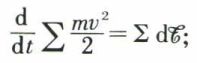

en intégrant, on a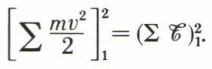

Cette équation exprime le théorème absolument général des forces vives. La variation de la force vive totale du système, entre les temps 1 et 2, est égale à la somme des travaux de toutes les forces du système, tant extérieures qu’intérieures ou de liaison, dans le même intervalle de temps.

Mais, avec l’équation (I), l’intégration est impossible. Le théorème des forces vives ne s’applique donc que si l’on tient compte du travail des liaisons. Il y a donc apparemment un paradoxe sur le théorème des forces vives.

L’emploi du principe du travail virtuel comme procédé analytique d’expression de l’équilibre des vecteurs élimine les liaisons qui, par hypothèse, ne travaillent pas. Mais de telles liaisons, en supposant les déplacements compatibles avec leurs valeurs au temps t (déplacements virtuels), peuvent travailler quand il s’agit de déplacements réels. D’où ce paradoxe suivant lequel le théorème des forces vives, qui est pourtant absolument général, semble ne plus s’appliquer quand les liaisons varient avec le temps. Cela tient à ce que, en étudiant les déplacements virtuels, on supprime automatiquement le travail de ces liaisons, travail qui n’est généralement pas nul quand ces liaisons varient avec le temps. Bien entendu, la variation de force vive des masses n’est pas égale au travail des forces qui ne sont pas conventionnellement des forces de liaison, c’est-à-dire que le procédé de calcul n’élimine pas ; il faut ajouter le travail des forces de liaison.