invariance (suite)

Produits CP et CPT

Le produit CP pourrait conduire à une invariance dans les interactions faibles, bien que les opérations C et P effectuées séparément n’assurent pas l’invariance des propriétés. Mais on a observé dans la désintégration des mésons K neutres (méson K° à vie longue se désintégrant en un pion positif et un pion négatif) qu’il n’y avait même pas conservation du produit PC. Il reste cependant que deux systèmes physiques déduits l’un de l’autre par le produit des trois réflexions CPT ont les mêmes propriétés. C’est en particulier ce que prouvent l’identité des périodes de désintégration du muon positif et du muon négatif, la comparaison des probabilités de diffusion des deutons et des antideutons sur les protons ou encore la mise en évidence de noyaux d’antihélium 3. Il s’agit là d’un résultat très général de la théorie des champs qui établit l’invariance CPT conduisant à l’indiscernabilité entre des particules et leurs antiparticules associées par le produit de réflexions CPT : la particule en mouvement et l’antiparticule animée du même mouvement dans le sens inverse du temps ont même énergie totale, même impulsion totale et donc même masse au repos ; elles ont éventuellement même période de désintégration.

Les transformations unitaires

Symétries U (1)

À côté des symétries qui dépendent des propriétés de l’espace-temps, il y en a d’autres qui font intervenir les variables internes, c’est-à-dire les paramètres autres que la masse et le spin, qui sont laissés invariants dans toutes les transformations d’espace-temps. Les plus simples de ces symétries sont associées à des invariances absolues et sont représentées par le groupe des symétries unitaires d’ordre 1. Elles correspondent chacune à un nombre quantique additif conservé dans toutes les interactions et changeant de signe dans la conjugaison de charge C. Les transformations qui font apparaître ces invariances de variables internes sont des transformations de jauge modifiant la phase des champs décrivant la particule considérée d’une quantité proportionnelle à cette variable.

• Conservation de la charge électrique Q. Elle correspond à l’invariance de jauge dans l’« espace de charge », ou « espace de spin isotopique ». Dans les processus physiques, en effet, les charges électriques apparaissent et disparaissent par paires, et l’univers reste électriquement neutre.

• Conservation du nombre baryonique B. Cette nouvelle variable interne a été introduite pour rendre compte de la conservation de là matière nucléaire : le nombre de nucléons reste constant, la création ou l’annihilation de particules ne se faisant que par paires nucléon-antinucléon. La conservation du nombre baryonique s’applique aussi aux hypérons et aux noyaux ; le nombre de baryons reste constant dans l’univers. Seuls parmi les hadrons, les mésons ont un nombre baryonique nul et peuvent apparaître en nombre quelconque dans une collision entre baryons.

• Conservation du nombre leptonique L. Il semble qu’on puisse distinguer un nombre leptonique électronique L_e, qui traduit la conservation du nombre global d’électrons, positrons, neutrinos électroniques et anti-neutrinos électroniques, et un nombre leptonique muonique L_μ jouant le même rôle pour les muons et les neutrinos muoniques, ou neutrettos. Ces nombres L_e et L_μ sont nuls pour toutes les particules autres que les leptons. Il est certain en tout cas qu’il y a conservation du nombre leptonique L = L_e + L_μ.

• Conservation de l’étrangeté S. Bien qu’il s’agisse d’une invariance partielle puisque non respectée par les interactions faibles, il est logique d’associer aux autres invariances de jauge la conservation de l’étrangeté, qui traduit le fait que les particules « étranges » sont produites par paires. L’étrangeté S, nombre quantique introduit par Murray Gell-Mann et K. Nishijima, est bien définie pour tous les hadrons. On utilise plus souvent l’hypercharge Y, somme de l’étrangeté et du nombre baryonique : Y = B + S, dont l’invariance est associée à l’inversion, ou renversement du sens, des coordonnées dans l’espace de charge.

Symétrie SU (2)

Le formalisme du « spin isotopique », ou « isospin », a été introduit par similitude avec le formalisme du spin dans l’espace ordinaire, pour exprimer le fait que le neutron et le proton apparaissent comme deux états de charge d’une même particule, le nucléon. On constate en effet que les interactions fortes entre deux protons sont presque identiques aux interactions entre un proton et un neutron. C’est le principe de l’indépendance de charge des forces nucléaires. On imagine alors un espace à trois dimensions, l’espace de charge, dans lequel le groupe des rotations laisse invariantes les interactions fortes. La variable interne considérée, le spin isotopique I, a trois composantes, la troisième I_z étant reliée à l’hypercharge et à la charge électrique par la relation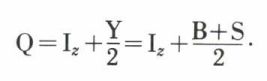

La quantité est conservée dans toutes les interactions, alors que les interactions faibles ne conservent pas I_z — pas plus qu’elles ne conservent Y ou S et que le spin isotopique total n’est conservé que dans les interactions fortes. C’est la composante I_z qui repère les (2I + 1) membres d’un multiplet défini par I² et des valeurs données de B et S. Outre le cas déjà cité des deux états du nucléon, correspondant à on peut donner l’exemple des trois états du pion (π⁺, π⁰, π^–) correspondant à I = 1.

Le principe de symétrie de charge, selon lequel les interactions fortes entre deux protons sont sensiblement égales à celles entre deux neutrons, introduit une nouvelle transformation qui change par exemple un proton en neutron, renversant le sens de I_z : c’est une rotation d’angle π autour de l’axe I_y.

Si on associe cette réflexion avec l’opération de conjugaison de charge, C, on obtient la parité G. La symétrie de charge et la parité G sont deux invariances respectées seulement par les interactions fortes. L’intérêt de la parité G se manifeste dans le cas où B = S = 0, donc Q = I_z, et où elle offre une expression commode de l’invariance par conjugaison de charge : on a le produit de deux opérations, la symétrie de charge et C, dont chacune renverse le sens de I_z = Q ; le résultat est donc l’invariance de I_z.