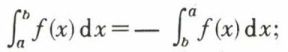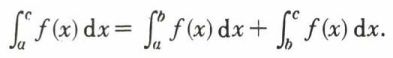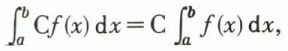Éd. 1971-1976

insuline (suite)

C. Fruteau de Laclos, les Insulines retard (Varia, 1955). / M. E. Krahl, The Action of Insulin on Cells (New York et Londres, 1961). / D. Perez Garcia, The Biochemical Effects of Insulin which are used in Therapy (Mexico, 1963). / J. Quevauvilliers, L. Perlemuter, P. Obraska et A. Kopf, Cahiers de biologie, t. I : Circulation, rein, endocrinologie (Masson, 1965 ; 3^e éd., 1972). / J. Trémolières, G. Tchobroutsky, J. L. de Gennes et coll., Nutrition et métabolisme (Flammarion, 1971).

Les savants qui ont découvert l’insuline

John Jacob Abel,

pharmacologiste et biochimiste américain (Cleveland 1857 - Baltimore 1938). En 1926, il obtint une insuline pure et cristallisée.

Frederick Grant Banting,

physiologiste canadien (Alliston, Ontario, 1891 - Musgrave Harbour 1941). Il a isolé l’insuline des îlots de Langerhans du pancréas à l’université de Toronto, où il travaillait avec Best, Collip et Macleod. Il a partagé avec ce dernier le prix Nobel de médecine en 1923 pour leur découverte.

Charles Herbert Best,

physiologiste canadien (West Pembroke, Maine, 1899). Après avoir travaillé avec Banting à la découverte de l’insuline, il a étudié l’histamine, la choline, l’héparine. On lui doit The Physiological Basis of Medical Practice (1939).

James Bertran Collip,

biochimiste canadien (Toronto 1892 - † 1959). Il participa à l’isolement de l’insuline et s’illustra par la découverte de l’hormone de la parathyroïde*.

Panayotis G. Katsoyannis,

biochimiste américain, d’origine grecque (né en 1924). Il a réussi la synthèse des chaînes A et B de l’insuline en 1963.

John James Rickard Macleod,

physiologiste écossais (près de Dunkeld, Perthshire, 1876 - Aberdeen 1935). Il fut assistant au London Hospital, puis professeur à Cleveland et à Toronto, où il collabora avec Banting à l’isolement de l’insuline. Il partagea avec lui le prix Nobel de médecine en 1923.

Frederick Sanger,

biochimiste britannique (Rendcomb, Gloucestershire, 1918). Il a élucidé en 1955 la structure de l’insuline, montrant qu’elle était composée de deux chaînes polypeptidiques réunies en deux points par des radicaux sulfhydriques. Il a obtenu le prix Nobel 1958 pour la découverte de l’enchaînement des amino-acides de l’insuline.

Helmut Zahn,

chimiste allemand (Erlangen 1916). Il a réussi peu après Katsoyannis à synthétiser les deux chaînes de l’insuline et à les réunir en un seul peptide en 1963, obtenant ainsi un produit physiologiquement actif.

intégrale définie

Limite, si elle existe, de la somme

quand le nombre des quantités x_p augmente indéfiniment, le plus grand des intervalles (x_p, x_p+1) tendant vers zéro, et f étant une fonction réelle définie et bornée sur le segment [a, b].

Les nombres x_p tels que
x₀ = a < x₁ < ... < x_p < x_p+1 < ... < x_n < b = x_n+1
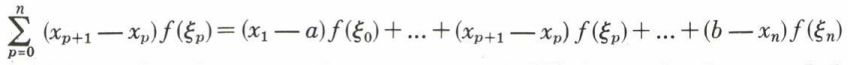
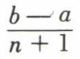partagent le segment [a, b] en n + 1 intervalles que l’on peut prendre égaux entre eux et à ; le nombre ξ_p appartient à l’intervalle (x_p, x_p+1). Si 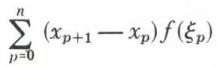tend vers une limite I, dans les conditions indiquées, on dit que la fonction f est intégrable au sens de Riemann sur le segment [a, b] ; le nombre I s’appelle l’intégrale de f sur le segment [a, b] et est désigné par la notation de Fourier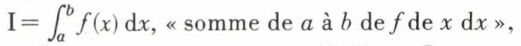

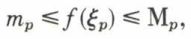
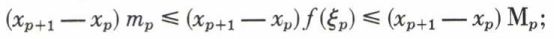
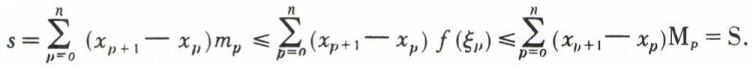
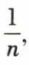cette notation rappelant comment est obtenue la limite I.

Condition d’intégrabilité

La fonction f, étant supposée bornée sur le segment [a, b], admet sur chaque intervalle (x_p, x_p+1) une borne inférieure m_p et une borne supérieure M_p et l’on a

d’où, puisque x_p+1 – x_p > 0,

par suite,

Il suffit alors, pour que I existe, que les sommes s et S tendent vers une même limite, qui sera alors la limite I.

Or, et c’est le théorème de Darboux, quand n augmente indéfiniment, les sommes s et S tendent respectivement vers les limites I′ et I″, pourvu que la plus grande des différences x_p+1 – x_p tende vers zéro. De plus,

par suite, pour que I′ = I″ = I, il suffit que S – s tende vers zéro ; il suffit, par exemple, qu’il existe une suite de nombres positifs ℰ_n tendant vers zéro avec telle que, pour chaque subdivision de [a, b] en n + 1 intervalles, on ait S – s < ℰ_n ; c’est la condition d’intégrabilité de Riemann.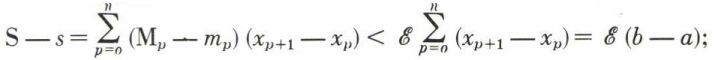

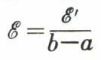Exemples de fonctions intégrables

• Toute fonction continue sur un segment est intégrable sur ce segment.

En effet, si f est une fonction continue sur [a, b], elle y est uniformément continue : pour tout couple (x, x′) tel que | x – x′ | < η), on a | f (x) – f (x′) | < ℰ, ℰ ne dépendant que de η. Si on prend toutes les différences x_p+1 – x_p inférieures à η, on aura M_p – m_p < ℰ quel que soit p ; par suite,

il suffit alors de prendre pour que S – s soit inférieure à ℰ′, ℰ′ étant une quantité arbitrairement petite, fixée à l’avance. Il en résulte alors que S – s → 0 et que la limite I existe.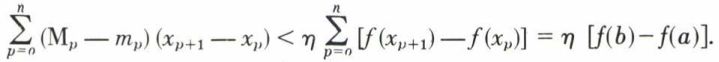

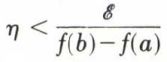• Toute fonction monotone sur [a, b] est intégrable. Si f est croissante sur [a, b] ou même simplement non décroissante, sur chaque intervalle (x_p, x_p+1) on a m_p = f (x_p) et M_p = f (x_p+1) ; par suite, l’inégalité x_p+1 – x_p < η) entraîne

Il suffit alors de prendre pour que S – s soit inférieure à ℰ ; ainsi, S – s → 0 de la limite I existe.
On fait une démonstration analogue si f est non croissante.

Propriétés de l’intégrale définie

1. Si b < a,
par suite, on peut intervertir les bornes d’intégration dans une intégrale définie à condition de changer le signe devant l’intégrale.

2. Si f est intégrable sur (a, b) et sur (b, c), a < b < c, elle l’est sur (a, c) et l’on a

Cette formule se généralise à trois nombres quelconques.

3. Si f est intégrable sur (a, b), Cf l’est aussi, et

C étant une constante.