information (suite)

La théorie de l’information

Il est nécessaire de faire une distinction très nette entre d’une part l’information, qui est la matière première et ne consiste qu’en une simple collection de données, et d’autre part le savoir, qui suppose une certaine intelligence, nécessaire pour la comparaison, la classification et l’exploitation de ces données. Pour édifier une théorie de l’information, la première tâche à réaliser est une approche plus précise du concept. Acquérir une information est, en toute généralité, lever une incertitude sur l’état d’un système. Un système en général est parfaitement défini lorsqu’on connaît les différents états qu’il peut prendre et les différentes probabilités qu’il a de prendre ces états. À partir de ces probabilités, on peut définir l’information comme une quantité mesurable, ce qui satisfait le scientifique et plus particulièrement le mathématicien.

Chaque système est décrit par une collection de données statistiques, qui sont les mêmes pour tous les observateurs. Une définition de l’information ne prenant en compte que les données et leurs probabilités est donc absolument objective et indépendante de l’observateur. En revanche, la valeur de l’information est un élément subjectif : telle information, contenue dans la même phrase, peut être pour une certaine personne d’une extrême importance et sans intérêt pour les autres, voire ne pas avoir la même signification pour deux personnes différentes, comme c’est le cas des messages codés.

Quantité d’information

Dans un système qui peut se trouver dans des états distincts, A₁, A₂,..., A_n avec des probabilités respectives p₁, p₂, ..., p_n, un tirage au sort fixe l’état A_i de ce système. Avant le tirage, il existe une incertitude sur le résultat ; après le tirage, cette incertitude est levée et l’on a acquis une certaine quantité d’information. Incertitude et quantité d’information dépendent évidemment de la loi de probabilité du tirage, c’est-à-dire des probabilités {p_j}. Dans un tirage au sort où il n’y a que deux résultats, A₁ et A₂, les trois cas suivants se classent dans l’ordre des incertitudes décroissantes :

La quantité d’information acquise par le tirage doit aller en décroissant selon les trois cas.

On a donc été amené à définir une fonction dépendant des probabilités des différents résultats et donnant une mesure raisonnable de l’incertitude d’un tirage ou, ce qui est équivalent, de la quantité d’information qu’il apporte. Une fonction, appelée entropie de la loi de probabilité considérée, aboutit à ce résultat.

Elle est définie par la formule :

Les probabilités p_j étant comprises entre 0 et 1, la fonction H est toujours positive ou nulle. Elle est définie à une constante multiplicative près, qui est fixée lorsqu’on choisit la base du logarithme. La base la plus communément adoptée est la base 2, auquel cas l’entropie est exprimée en bits. On se sert d’une manière moins courante de la base 10, auquel cas l’unité est le hartley, et de la base e, auquel cas l’unité est le neper.

Dans le cas de deux éventualités A₁, et A₂ de probabilités p et q = 1 – p, l’entropie H₂ (p, q) a pour valeur :
H₂ (p, q) = – p log₂ p – q log₂ q,
log₂ x représentant le logarithme de x dans la base 2.

L’équiprobabilité correspond à l’entropie maximale, qui est de 1 bit. Le bit est donc la quantité d’information correspondant au résultat du tirage au sort entre deux éventualités de même probabilité.

Propriétés de la fonction d’entropie

La fonction H introduite par la formule (1) possède les propriétés suivantes, que le sens commun réclame.

Propriété A. La fonction
H(p₁, p₂, ..., p_n)
est égale à zéro si et seulement si toutes les probabilités « p_j » sont nulles, à l’exception de l’une seule d’entre elles, qui vaut nécessairement 1.

Cette propriété correspond au sens commun, selon lequel l’arrivée d’un événement certain n’apporte aucune information. Il suffit de se reporter à la formule (1) pour voir que la fonction H, formée d’une somme de termes positifs ou nuls, ne peut être nulle que si tous les termes sont nuls, ce qui implique à son tour que les éléments p_i soient nuls, sauf un seul, égal à 1.

Propriété B.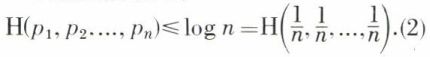

Cette propriété signifie en langage courant que l’incertitude est la plus grande quand tous les événements possibles ont même probabilité.

Propriété C. Additivité des quantités d’information relatives à deux tirages.

Si l’on réunit deux tirages au sort, A (n cas possibles) et B (m cas possibles), on constitue un seul tirage comportant un nombre d’éventualités égal à n.m. Ce tirage, appelé tirage produit des tirages A et B, est symbolisé par (AB). Il y a naturellement une relation entre les quantités d’information apportées par le tirage A, le tirage B et leur tirage produit. En particulier, si les deux tirages A et B se rapportent à des événements sans relation entre eux, c’est-à-dire si A et B sont des tirages indépendants, la quantité d’information du tirage produit (AB) est la somme des quantités d’information respectivement données par les tirages A et B :

En revanche, si les tirages A et B sont liés, la quantité d’information relative au tirage AB est inférieure à la somme des quantités d’information dès tirages A et B :

La fonction d’entropie satisfait à toutes ces propriétés, et en particulier dans le cas extrême où le résultat de A détermine complètement le résultat de B :

c’est-à-dire que la quantité d’information du tirage produit est égale à celle du tirage A, ce qui, encore une fois, satisfait le sens commun. Dans le cas le plus général, on introduit l’entropie conditionnelle H_A(B) qui correspond à la quantité d’information apportée par le tirage B quand le tirage A est réalisé.

ce qui correspond au fait que connaître le résultat d’un tirage A ne peut que faire décroître l’incertitude d’un tirage B.

La fonction entropie, telle qu’elle est définie par la formule (1), est la seule fonction, continue par rapport à toutes ses variables, qui possède les deux propriétés fondamentales résumées par les formules (2) et (7). De plus, elle répond à toutes les conditions intuitives posées par le concept de quantité d’information.