Conifères (suite)
Comme espèces servant au reboisement, on peut citer de nombreux Pins : le Pin sylvestre, très répandu dans toute l’Europe ; le Pin à crochets, qui résiste dans les conditions rudes des montagnes européennes ; le Pin Laricio, dont on remarque trois races géographiques (les Pins d’Autriche, de Corse et de Salzmann, ce dernier se localisant dans les Pyrénées orientales, l’Espagne et l’Afrique du Nord) ; le Pin d’Alep, vivant surtout dans tout le Bassin méditerranéen, et le Pin maritime, qui a servi au peuplement des Landes au xixe s.
D’autres genres et espèces servent également, en premier lieu les Sapins, entre autres Abies pectinata, assez abondant dans les montagnes françaises mais aussi en Europe centrale et dans les Balkans ; Abies pinsapo et A. numidica, qui sont surtout utilisés dans les basses montagnes des régions méditerranéennes, et Abies grandis, originaire de l’ouest des États-Unis (Vancouver), qui donne de bons résultats dans le Massif central et en Bretagne ; puis Pseudotsuga Douglasii (douglas), qui est une espèce très fréquente en Amérique du Nord, divers Épicéas et Mélèzes, ainsi que les Cèdres de l’Atlas, qui, malgré des difficultés d’implantation dans les premières années, donnent des résultats parfois remarquables dans les basses montagnes méditerranéennes.
Enfin, quoique plus fréquemment employés comme arbres d’ornement, on peut citer en particulier les Thuyas, les Chamaecyparis, les Séquoias et les Cyprès chauves (Taxodium), qui vivent dans les marécages peu profonds et qui possèdent de curieuses racines pneumatophores dont certaines excroissances sortent à l’air libre de la vase, tous arbres de l’Amérique du Nord. Une mention doit être faite du Cyprès de Lambert, dont le peuplement d’origine est particulièrement réduit sur la côte californienne mais qui est maintenant une espèce extrêmement répandue sur les côtes atlantiques, où il sert d’arbre d’ornement et de coupe-vent.
J.-M. T. et F. T.
L. Pardé, les Conifères (La Maison Rustique, 1937 ; nouv. éd., 1948). / V. Chaudun, Conifères d’ornement (La Maison Rustique, 1956). / J. Pourtet, les Repeuplements artificiels (École nationale des eaux et forêts, Nancy, 1965). / C. Testu, Conifères de nos jardins (La Maison Rustique, 1970).





 de la matrice
de la matrice 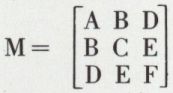 y joue un rôle :
y joue un rôle :

 : la conique est non dégénérée ; les pentes des directions asymptotiques sont les racines de l’équation m2 – 2 = 0, c’est-à-dire
: la conique est non dégénérée ; les pentes des directions asymptotiques sont les racines de l’équation m2 – 2 = 0, c’est-à-dire 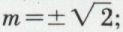 le centre a des coordonnées qui vérifient le système – 2x + 6 = 0, y + 2 = 0, dont la solution est x0 = 3, y0 = – 2 ; la conique est une hyperbole dont l’équation s’écrit (y + 2)2 – 2(x – 3)2 + 18 = 0, ce qui met en évidence la nature, le centre et les asymptotes de la conique.
le centre a des coordonnées qui vérifient le système – 2x + 6 = 0, y + 2 = 0, dont la solution est x0 = 3, y0 = – 2 ; la conique est une hyperbole dont l’équation s’écrit (y + 2)2 – 2(x – 3)2 + 18 = 0, ce qui met en évidence la nature, le centre et les asymptotes de la conique.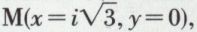 d’où le nom d’ellipse imaginaire.
d’où le nom d’ellipse imaginaire.