classe et relation (suite)

Un calcul des relations

Dans la mesure où toute relation est une classe, le calcul des relations sera isomorphe à celui des classes. C’est ainsi que, si R et S sont des relations, si, par exemple, R = df { xy | A (x,y) } et S = df { xy | B (x,y) }, on pourra poser

c’est-à-dire que deux relations sont égales si et seulement si elles contiennent les mêmes couples. Cette définition, comme celle, analogue, de l’égalité des classes, rend certaines distinctions impossibles. Supposons, par exemple, que les cinq nombres de la classe α = df { 0,1,2,3,4 } soient ordonnés par valeurs croissantes sur un axe de gauche à droite. Posons A (x,y) = df x est à gauche de y et B (x,y) = df x est plus petit que y. Dans ces conditions, les relations R et S définies ci-dessus ont la même extension, et, partant, elles sont indistingables.

On aura aussi la relation d’inclusion entre relations

Ainsi, toujours sur la classe α et en adoptant les relations usuelles, on a

Il est encore possible d’étendre comme suit les opérations d’intersection, d’union et de complément :

L’union, l’intersection et le complément des relations sont des opérations peut-être moins souvent utilisées que leurs homologues sur les classes. Il est cependant possible d’en donner des exemples. Si R = df être père de et S = df être mère de, alors R ∪ S = df être parent de. Si R = df être plus petit ou égal à et S = df être plus grand ou égal à, et si R et S sont, disons, toutes deux définies sur la même classe de nombres, alors R ∩ S = df être égal à. Quant à ce sera évidemment la relation ≠.

On peut enfin définir la relation vide et la relation totale, que nous notons comme les classes correspondantes, mais en les pointant :

Le fait que les relations sont des classes de couples et non des classes d’objets permet d’introduire des opérations qui leur sont propres. Soit, par exemple, R la relation de parent à enfant. Cela signifie, comme nous l’avons vu, que, si (x,y) ∈ R, x est père ou mère de y. Mais, inversement, y est fils ou fille de x. Il s’ensuit que la classe des couples (y,x) définit la relation d’enfant à parent, que nous appellerons l’inverse de R et que nous noterons R^–1. Nous poserons donc

Si donc (x,y) ∈ R^–1 alors, par l’expression (* *), on a (y,x) ∈ R.

Il sera commode, dès maintenant, d’introduire une notation plus proche de l’écriture usuelle en décidant d’écrire xRy au lieu de (x,y) ∈ R. La définition de l’inverse conduit donc à la loi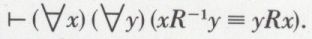

Cela signifie, avec notre exemple, que, pour tout x et pour tout y, si x est enfant de y, alors y est parent de x et réciproquement.

Considérons maintenant les deux relations R = df être père de et S = df être femme de. Il peut arriver que, parmi les couples qui appartiennent à R, il s’en trouve un, disons (x,z) tel que z soit une femme et que z soit également le premier terme d’un couple qui appartient à S, disons le couple (z,y). Dans ces conditions, il existe une relation T entre x et y, à savoir que x est le beau-père de y. Cette relation T est le produit de R et S dans cet ordre :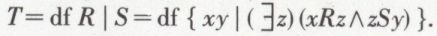

On aura donc

L’opération produit de relations est associative, mais il faut prendre garde qu’elle n’est généralement pas commutative. Ainsi, dans l’exemple précédent, x(R | S)y = df x est le père de la femme de y = df x est le beau-père de y, tandis que x(S | R)y = df x est la femme du père de y, c’est-à-dire sa mère ou sa belle-mère.

Le produit et l’inverse sont liés par une loi remarquable qui est la suivante :

En effet, x(R | S)^–1y équivaut à y(R | S)x, soit encore à D’autre part, x(S^–1 | R^–1)y est équivalent à ou encore à et enfin, puisque la conjonction est commutative, à

Rien n’empêche de faire aussi le produit d’une relation par elle-même et de généraliser. On aura R² = df R | R, R³ = df R² | R, etc.

Pour être à même d’utiliser sans restriction les exposants des relations, il faut encore définir R¹ = dfR et R⁰.

Pour cela, nous allons introduire trois classes associées à toute relation : le domaine, le codomaine et le champ. Le domaine de R, Dom(R), est la classe des premiers termes des couples de R, le codomaine de R, Cod(R), est la classe des seconds termes des couples, et le champ de R, Ch(R), est l’union du domaine et du codomaine :

Nous poserons alors R⁰ = df { xy | x = y ∧ x ∈ Ch(R) }. En d’autres termes, la relation R⁰ est la relation d’identité entre les objets qui sont en relation R les uns avec les autres. En résumé, on a

On peut établir les deux lois suivantes :
Quelle que soit la relation R et si m et n sont positifs,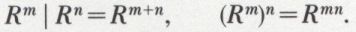

Si R est une relation biunivoque, quels que soient m et n,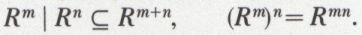

Quelques propriétés des relations

Soit R la relation de parallélisme entre les droites du plan. Si la droite x est parallèle à la droite y, il s’ensuit que la droite y est parallèle à la droite x.

On dit que R est une relation symétrique :

Si une relation est symétrique, son inverser l’est aussi : Sym(R) ↔ Sym(R^–1).

Une relation peut ne pas être symétrique de deux façons. Ou bien la chose est impossible, comme pour la relation « être père de », et l’on dit que la relation est asymétrique, ou bien elle n’est symétrique que pour certains couples, et l’on dit qu’elle est non symétrique. Tel serait le cas de la relation « être frère de ». Si x est frère de y, y n’est frère de x que si y est un garçon. On aura

Relativement à la symétrie, les relations peuvent donc se répartir comme le montre le schéma suivant :

La non-asymétrie se définit naturellement en niant l’asymétrie :

ce qui équivaut à