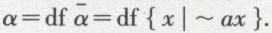classe et relation

Intuitivement, une classe est une collection d’objets. D’une façon plus rigoureuse, on peut caractériser une classe logique en l’associant à une forme propositionnelle qui contient une seule variable libre. La classe constitue alors l’extension de la forme propositionnelle.
Intuitivement, une relation est ce qui détermine deux objets l’un par rapport à l’autre. En logique, une relation est l’extension d’une forme propositionnelle qui contient plus d’une variable libre. Elle sera dite binaire si la forme propositionnelle contient deux variables libres distinctes, ternaire si elle en contient trois, etc.

La notion de classe

Partons d’une forme propositionnelle à une mention d’objet (v. calcul des prédicats) et soit, pour fixer les idées, ax = df x est un nombre naturel. La variable d’objets x prend ses valeurs sur un certain domaine Ω, que nous appellerons l’univers du discours. Dès lors, ax permet d’effectuer une partition de Ω en deux domaines. En effet, si x₁ est un objet qui appartient à Ω, deux cas peuvent se présenter :
(1) la proposition ax₁ est vraie ;
(2) la proposition ax₁ est fausse.
Il s’ensuit que les x_i tels que ax_i est vraie déterminent une classe, à savoir ici celle des nombres naturels. Conformément à l’usage algébrique, nous noterons cette classe { x | ax }, ce que nous lirons « les x tels que ax » ou encore, dans notre exemple, « les x tels que x est un nombre naturel ».

Il faut noter que, sur le plan formel, la variable x qui figure dans la notation { x | ax } est une variable liée ou apparente. Cela fait que l’on pourrait tout aussi bien désigner cette classe par { y | ay }, { z | az } ou même { . | a. }. À cela correspond la possibilité de remplacer la locution « les x tels que x est un nombre naturel » par « les nombres naturels ».

Remarque

Il n’y a pas de difficultés à accepter que, quel que soit l’univers du discours choisi, il y a un sens à se demander si l’un quelconque de ses éléments est ou n’est pas un nombre naturel. Mais considérons le prédicat b = df avoir un poids. Dans ces conditions, si Ω contient l’objet « Dieu », l’expression b(Dieu), soit « Dieu a un poids », n’a pas de sens. On pourrait donc penser que bx_i peut non seulement être une proposition vraie ou fausse, mais n’avoir pas de sens du tout. En fait, une telle objection ne doit pas nous arrêter. Elle repose en effet sur des considérations qui sortent du cadre de la logique formelle, dans la mesure où elle fait nécessairement appel à des connaissances extérieures à la logique, disons ici à des connaissances théologiques.

D’une façon générale, la logique des prédicats étant supposée donnée, à toute forme propositionnelle A (x), qui contient la seule variable d’objets libre x, nous allons tenter d’associer une classe, celle des x tels que A (x), c’est-à-dire la classe α = df { x | A (x) }. Intuitivement, dire alors que « x est A » ou dire que « x est élément de α » sont deux expressions équivalentes. Si l’on introduit donc la relation d’appartenance ∈, il est possible de poser

Comme nous avons vu que α peut tout aussi bien s’écrire { y | A (y) }, on aura encore

Cette façon de procéder est cependant trop libérale, comme le fait voir l’exemple suivant.

Soit A (y) = df ~ (y ∈ y) et soit α = df { y | ~ (y ∈ y) } la classe associée à la forme propositionnelle. On aura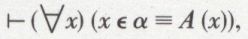

soit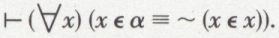

Cette dernière expression est censée être vraie pour tout x, donc en particulier aussi pour ce nouvel objet de pensée qui est α. On pourra donc écrire, en éliminant le quantificateur universel et en substituant α à x,

Notons que α ∈ α est une proposition et désignons-la par p. On aura donc

Le calcul des propositions fournit, de son côté, le théorème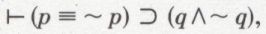

et, par la règle du modus ponens (v. calcul des propositions), il vient

Ainsi, une logique qui, en plus des schémas d’axiomes usuels, introduirait une expression de la forme (*) serait contradictoire. Il s’agit de la fameuse antinomie de Russell (1903), qui a momentanément remis en cause la tentative de formaliser les mathématiques. Il convient donc de prendre des mesures propres à limiter la portée de l’expression (*) et de ne pas considérer qu’à toute forme propositionnelle on a le droit d’associer une classe. C’est ce à quoi sert par exemple la théorie des types, créée par B. Russell (1908) et simplifiée par F. P. Ramsey (1926). Pour exprimer les choses simplement, la théorie s’interdit, en particulier, de placer le signe ∈ entre des objets de même type : entre deux variables d’objets ou entre deux variables de classes par exemple. Les différents êtres logiques sont hiérarchisés, et la relation d’appartenance ∈ n’est légitime qu’entre des niveaux appropriés.

Un calcul des classes

Si l’on admet que toutes précautions sont prises pour éviter l’antinomie de Russell et que d’autres sont encore possibles (E. W. Beth 1955), il est alors facile de construire un calcul des classes à partir de celui des prédicats.

Désignons par α, β, γ, etc., les classes légitimement associées aux variables de prédicats à une place et posons, par exemple :

Nous poserons d’abord que deux classes sont égales si et seulement si elles contiennent les mêmes éléments :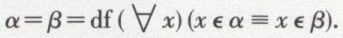

On aura donc aussi

soit enfin par (*)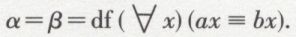

Cela fait voir que la classe α associée au prédicat a n’est rien d’autre que son extension. Il s’ensuit que, si, par exemple, on a ax = df x est un triangle équilatéral et si bx = df x est un triangle équiangle, la classe des triangles équilatéraux n’est pas distinguable de celle des triangles équiangles.

On montre que la relation d’égalité ainsi définie — et qu’il ne faut pas confondre avec celle d’identité entre variables d’objets aussi notée = — est une relation d’équivalence.

Cela dit, on peut construire un calcul élémentaire des classes à l’aide de deux constantes et de trois opérations. Les constantes sont la classe vide, notée ∧, et la classe totale, notée ∨ :

On montre que la classe vide ne contient aucun élément, donc que 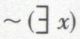(x ∈ ∧), et l’on voit que la classe totale n’est rien d’autre que l’univers du discours. Quant aux opérations, ce sont celles d’intersection, d’union et de complément. Elles sont définies comme suit :
α intersection β = df α ∩ β = df { x | ax ∧ bx } ;
α union β = df α ∪ β = df { x | ax ∨ bx } ;
complément de