cinématique (suite)
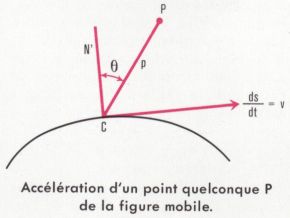
Accélération d’un point quelconque P de la figure mobile. La composante tangentielle est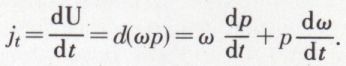
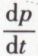 est la différence des projections sur CP des vitesses de P et de C. La vitesse de P, étant perpendiculaire à PC, a une projection nulle. Si θ est l’angle de CP avec la normale CN′, menée en C à la base du roulement, la projection de la vitesse est
est la différence des projections sur CP des vitesses de P et de C. La vitesse de P, étant perpendiculaire à PC, a une projection nulle. Si θ est l’angle de CP avec la normale CN′, menée en C à la base du roulement, la projection de la vitesse est 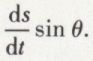 D’autre part,
D’autre part, 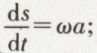 donc
donc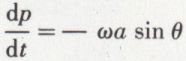
et, par suite,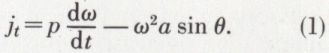
La composante centripète jn de l’accélération est dirigée suivant PC ; en appelant ρ le rayon de courbure de la trajectoire de P, on a 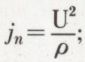 d’autre part, on a
d’autre part, on a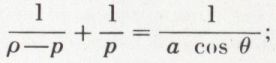
d’où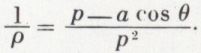
En remplaçant U par ωp, on obtient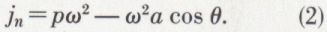
Les formules (1) et (2) montrent que l’accélération totale est la somme géométrique d’un vecteur 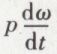 perpendiculaire à CP, d’un vecteur pω2 dirigé suivant PC et d’un troisième vecteur ω2a dirigé suivant CN′. L’ensemble des deux premiers équivaut à l’accélération d’un mouvement de rotation effectué autour du point fixe C avec la vitesse angulaire variable ω ; le troisième est l’accélération que possède le point C considéré comme appartenant à la figure mobile ; en effet, la vitesse de C, d’abord nulle, devient, au bout du temps dt, égale à CC1 × ω = ω2a dt, par suite de la rotation effectuée autour du nouveau centre instantané C1 ; la vitesse acquise dans le temps dt est donc égale à ω2a dt et perpendiculaire à CC1 ; enfin, l’accélération de C est égale à ω2a et dirigée suivant CN′. Dans le mouvement le plus général d’une figure plane invariable, dans son plan, l’accélération totale d’un point quelconque est, à chaque instant, la résultante de l’accélération due à la rotation autour du centre instantané et de l’accélération du point coïncidant avec ce centre instantané. En égalant à zéro les valeurs de jt et de jn, on trouve
perpendiculaire à CP, d’un vecteur pω2 dirigé suivant PC et d’un troisième vecteur ω2a dirigé suivant CN′. L’ensemble des deux premiers équivaut à l’accélération d’un mouvement de rotation effectué autour du point fixe C avec la vitesse angulaire variable ω ; le troisième est l’accélération que possède le point C considéré comme appartenant à la figure mobile ; en effet, la vitesse de C, d’abord nulle, devient, au bout du temps dt, égale à CC1 × ω = ω2a dt, par suite de la rotation effectuée autour du nouveau centre instantané C1 ; la vitesse acquise dans le temps dt est donc égale à ω2a dt et perpendiculaire à CC1 ; enfin, l’accélération de C est égale à ω2a et dirigée suivant CN′. Dans le mouvement le plus général d’une figure plane invariable, dans son plan, l’accélération totale d’un point quelconque est, à chaque instant, la résultante de l’accélération due à la rotation autour du centre instantané et de l’accélération du point coïncidant avec ce centre instantané. En égalant à zéro les valeurs de jt et de jn, on trouve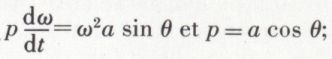
d’où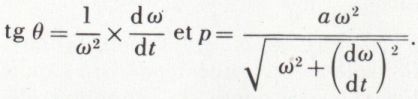
Ces valeurs de θ et de p déterminent un point unique dont l’accélération est nulle ; ce point porte le nom de centre d’accélération ; la relation p = a cos θ montre qu’il appartient à la circonférence d’inflexion ; son accélération étant nulle, il possède la même vitesse W aux deux instants t et t + dt. Si une translation uniforme de vitesse – W est imprimée à tout le système, elle ne modifie pas les vitesses acquises dans le temps dt et n’influe donc pas sur les accélérations, mais elle rend le centre d’accélération immobile. Par conséquent, les accélérations de tous les points de la figure sont les mêmes que si celle-ci tournait autour du centre d’accélération avec la vitesse angulaire ω ; l’accélération d’un point P situé à une distance r du centre d’accélération Q est la résultante d’une accélération rω2 dirigée suivant PQ et d’une accélération 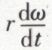 perpendiculaire à PQ.
perpendiculaire à PQ.
• Rotation autour d’un point. Le déplacement élémentaire d’un solide autour d’un point fixe équivaut à une rotation autour d’un axe instantané. Le déplacement continu s’obtient en faisant rouler sur un cône fixe un cône invariable lié au solide. La génératrice de contact des deux cônes est l’axe instantané de rotation. Si p, q, r désignent les composantes de la rotation instantanée ω, la vitesse du point (x, y, z) a pour composantes :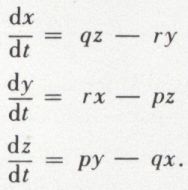
On a par ailleurs :
p2 + q2 + r2 = ω2.
Les composantes de l’accélération s’obtiennent en prenant la dérivée de  soit
soit 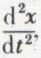 et en remplaçant
et en remplaçant 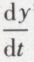 et
et 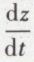 par leur valeur.
par leur valeur.
Par analogie avec la cinématique du point, on donne au vecteur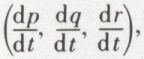
dérivée géométrique de la vitesse angulaire (p, q, r), le nom d’accélération angulaire. Dans le mouvement d’un solide autour d’un point fixe, l’accélération d’un point quelconque est, à chaque instant, le résultat de l’accélération due à la rotation instantanée (considérée comme constante en grandeur et en direction) et de la vitesse due à l’accélération angulaire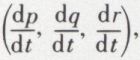
p, q, r étant les composantes de la vitesse du point quelconque x, y, z.
Points d’accélération nulle. Dans la rotation d’un solide autour d’un point fixe, il n’existe aucun point autre que le centre de rotation dont l’accélération soit nulle. De tels points ne peuvent exister en dehors de l’axe instantané de rotation, et il faut en outre que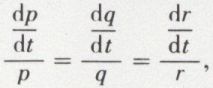
c’est-à-dire que p, q, r varient proportionnellement, autrement dit qu’à l’instant considéré la direction de l’axe instantané demeure stationnaire ; tous les points de cet axe ont alors une accélération nulle.
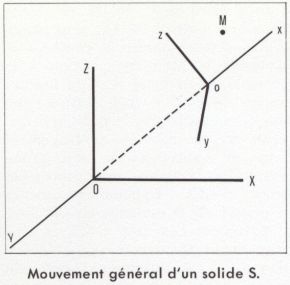
Mouvement général d’un solide S
Dans le cas général du déplacement d’un solide par rapport à un espace considéré comme fixe, on est conduit à concevoir un espace mobile entraîné par le solide S et faisant corps avec lui. Le moyen le plus rationnel de définir le mouvement d’un espace mobile est de se donner le mouvement d’un trièdre oxyz de coordonnées choisies dans cet espace et se déplaçant dans l’espace fixe matérialisé par un trièdre OXYZ de coordonnées fixes. L’objet de la cinématique du corps solide est de déduire du mouvement du trièdre mobile oxyz celui de tout point M invariablement lié à ce trièdre. Pour cela, on détermine la position de oxyz par rapport à OXYZ fixe, en définissant les composantes du vecteur 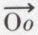 et, en outre, trois vecteurs unitaires,
et, en outre, trois vecteurs unitaires, 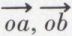 et
et 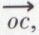 portés respectivement par ox, oy, oz. Du point de vue géométrique, le déplacement général d’un solide peut être considéré comme déterminé par une surface réglée, liée au corps solide, dont les génératrices viennent successivement en coïncidence avec celles d’une surface réglée fixe, avec, à chaque instant, rotation autour de la génératrice commune et glissement le long de cette génératrice, qui est appelée axe instantané de rotation et glissement. Si V est la vitesse de glissement et ω la vitesse de rotation, un point situé à la distance r de l’axe instantané a pour vitesse
portés respectivement par ox, oy, oz. Du point de vue géométrique, le déplacement général d’un solide peut être considéré comme déterminé par une surface réglée, liée au corps solide, dont les génératrices viennent successivement en coïncidence avec celles d’une surface réglée fixe, avec, à chaque instant, rotation autour de la génératrice commune et glissement le long de cette génératrice, qui est appelée axe instantané de rotation et glissement. Si V est la vitesse de glissement et ω la vitesse de rotation, un point situé à la distance r de l’axe instantané a pour vitesse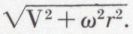
Pour calculer les projections de cette vitesse sur les axes fixes, en appelant (x0, y0, z0) les coordonnées d’un point déterminé A du corps, on passe d’une position à une position infiniment voisine en donnant au corps une translation dx0, dy0, dz0 qui amène A dans la position voulue ; on fait ensuite tourner le corps d’un angle ωdt autour d’une parallèle à l’axe instantané mené par A. Le déplacement réel est la somme géométrique des déplacements dus à la translation et à la rotation. En divisant par dt et en appelant x′0, y′0 et z′0 les dérivées de x0, y0 et z0, on trouve les formules pour les composantes de la vitesse du point de coordonnées (x, y, z). Dès lors, en dérivant les équations qui donnent U, V, W (composantes de la vitesse du point x, y, z), on calcule les composantes de l’accélération. On a d’ailleurs (p, q, r étant les composantes de ω) :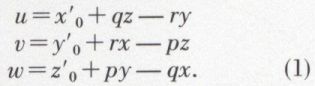
x′0, y′0, z′0, p, q, r sont des fonctions données du temps. La droite de l’espace représentée à l’instant t par la relation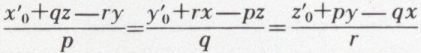
est l’ensemble des points pour lesquels la vitesse a la même direction que la rotation instantanée définie par (p, q, r) : c’est l’axe instantané de rotation et de glissement. En dérivant les équations (1), on obtient les composantes de l’accélération. Les formules obtenues ne diffèrent évidemment de celles qu’on obtient pour la rotation autour d’un point fixe que par la présence des termes x″0 y″0 z″0, correspondant à l’accélération de la translation. Dans le cas où la translation est rectiligne et uniforme, elle ne donne naissance à aucune accélération. Si, par exemple, le centre de gravité d’un corps se meut d’un mouvement rectiligne et uniforme, l’accélération d’un point quelconque du corps est exactement la même que si celui-ci tournait autour de son centre de gravité immobile.