calcul des propositions (suite)

Il est conforme à la plupart des usages de et de postuler que la proposition moléculaire « p et q » n’est vraie que si val (p) = val (q) = 1. Cela conduit à définir le foncteur de conjonction et, noté ⋀, par la table de vérité ci-dessous. On remarquera que, si l’on adopte une fois pour toutes l’ordre (1), (2), (3), (4) pour les valeurs de p et de q, on pourra définir le foncteur ⋀ par la donnée du quadruple ordonné (1 0 0 0).

En français, la disjonction est ambiguë. Si l’on dit, en effet, « Jean vous téléphonera ou vous écrira », il n’y a rien d’anormal à ce que Jean confirme son téléphone par une lettre. En revanche, il faudrait être un père dénaturé pour dire à son enfant « Tu mangeras ta soupe ou tu seras privé de dessert » et pour le priver de dessert après qu’il a mangé sa soupe. Cela conduit à distinguer deux foncteurs ou, le ou non exclusif, noté ⋁, et le ou exclusif, noté

La définition de la proposition conditionnelle « si p alors q » pose un problème, en ce sens que l’usage n’est pas clair. Soit, par exemple, la proposition « s’il fait beau dimanche, (alors) le match aura lieu ». Il est évident que la proposition moléculaire sera vraie si son antécédent (« il fait beau dimanche ») et son conséquent (« le match aura lieu ») sont tous deux vrais. Il est non moins évident que, si l’antécédent est vrai et le conséquent faux, la proposition moléculaire est fausse. Mais que faut-il poser en cas de mauvais temps ? À strictement parler, la proposition ne dit rien à ce sujet. Les organisateurs n’ont, si l’on peut dire, pris aucun engagement à ce sujet par leur déclaration. Ils peuvent donc librement maintenir le match ou le supprimer. Nous poserons donc que la proposition conditionnelle « si p alors q », que nous noterons « p ⊃ q », est vraie si val (p) = 0, et cela que q soit vraie ou fausse.

Si l’on voulait que, en cas de mauvais temps (p fausse), le match n’ait pas lieu, il faudrait dire « si et seulement s’il fait beau dimanche, (alors) le match aura lieu ». On aurait affaire à une proposition biconditionnelle, que nous noterions p ≡ q. Le foncteur ≡ est défini par la table ci-dessous :

Il est naturellement possible d’envisager des propositions moléculaires qui contiennent plus d’un foncteur. Il suffit, pour déterminer leur table de vérité, de procéder de proche en proche, comme le montre l’exemple ci-dessous. On notera que le foncteur de négation a été appliqué immédiatement et que les nombres encerclés indiquent l’ordre dans lequel les calculs ont été faits. Les parenthèses servent à préciser la façon de grouper les opérations.

Si l’on a affaire à une proposition moléculaire qui contient trois propositions atomiques p, q et m, il faudra envisager 2³ = 8 éventualités, comme le montre l’exemple ci-dessous. En général, l’étude d’une proposition dans laquelle figure n propositions atomiques exige une table de 2ⁿ lignes.

La façon de noter les divers foncteurs varie selon les auteurs. Le tableau suivant indique les principaux symboles.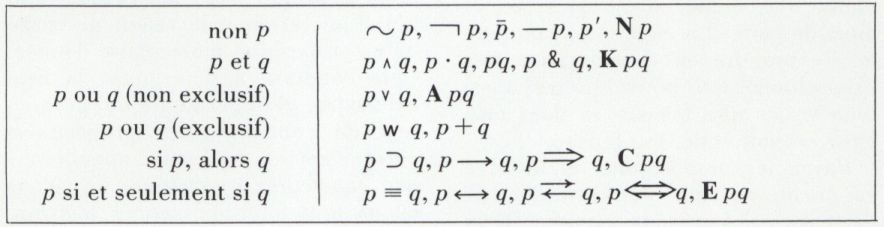

Remarque.

Les foncteurs binaires se placent entre leurs arguments, à l’exception de K, A, C, E. Ceux-ci sont dus à Łukasiewicz et constituent la notation polonaise. Elle offre l’avantage de rendre le « parenthésage » superflu, comme le montre l’exemple suivant :
Notation usuelle :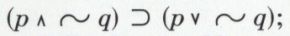

Notation polonaise : CK p N q A p N q.

Tautologies, implication, équivalence

Certaines propositions jouissent de la propriété remarquable de n’avoir que des 1 dans leur table de vérité. C’est, par exemple, le cas de la proposition p ⊃ (p ⋁ q), comme on peut le voir dans la table ci-dessous. De telles propositions sont donc vraies indépendamment des valeurs de vérité de leurs atomes.

En d’autres termes, et pour parler comme Leibniz, elles sont vraies dans tous les mondes possibles. Ce sont des lois logiques, et on les appelle des tautologies.

Désignons par les majuscules P, Q, M des propositions quelconques, atomiques ou moléculaires. Si une proposition P est une tautologie, nous écrirons ⊢ P. Ainsi, nous aurions ⊢ p ⊃ (p ⋁ q). Supposons alors que deux propositions P et Q soient telles que ⊢ P ⊃ Q. Dans ce cas, il existe une certaine relation entre P et Q, que nous appellerons relation d’implication. On pose
P → Q = df ⊢ P ⊃ Q = df
P implique Q.

Exemple. p implique p ⋁ q, soit p → (p ⋁ q), puisque ⊢ p ⊃ (p ⋁ q).

Il faut prendre garde à ne pas confondre le foncteur ⊃, qui, placé entre deux propositions, en engendre une troisième, et le signe →, qui, placé entre deux propositions, exprime une relation entre elles. Le signe ⊃ est un opérateur, tandis que le signe → est un relateur. L’analogie arithmétique suivante aidera à faire la distinction :

On introduit aussi la relation d’équivalence par la définition
P ↔ Q = df ⊢ P ≡ Q = df
P est équivalente à Q.

Exemple. p ⋀ q est équivalente à q ⋀ p soit (p ⋀ q) ↔ (q ⋀ p), puisque, comme on le vérifie sans peine, ⊢ (p ⋀ q) ≡ (q ⋀ p).

Les relations ↔ et → jouissent des propriétés suivantes :

Cela permet de dire que ↔ est une relation d’équivalence et que → est une relation d’ordre (partiel). [V. classes et relations.]

Dénombrement des foncteurs et organisation des propositions

Examinons la question de savoir quels sont tous les foncteurs binaires entre deux propositions p et q. On remarquera pour cela que chaque foncteur peut être envisagé comme une application de l’ensemble produit {1, 0} × {1, 0}, c’est-à-dire de l’ensemble des couples ordonnés {(1, 1),(1, 0),(0, 1),(0, 0)} vers l’ensemble {1, 0}. En conséquence, si l’on pose V = df {1, 0}, un foncteur binaire est une application
f : V × V → V.