asservissement ou système asservi (suite)

Si la trajectoire comporte une partie circulaire, avec la loi de commande PD, un écart non nul est nécessaire pour produire le braquage des roues requis par la courbe. Pour annuler cet écart permanent, il suffit d’introduire dans la loi de commande un terme proportionnel aux valeurs cumulées de l’écart, c’est-à-dire à son intégrale par rapport au temps (action proportionnelle, par dérivation et par intégration, ou PID). L’angle de braquage prend alors une valeur proportionnelle à l’intégrale de l’écart. Le choix du mode d’action à adopter dépend des propriétés dynamiques du système réglé. On utilise couramment les actions P, PD, PI (action proportionnelle et par intégration), I (action par intégration) et PID.

Théorie temporelle des systèmes asservis

La théorie mathématique des asservissements peut être présentée en utilisant comme variable soit le temps, soit la fréquence.

Une boucle d’asservissement est toujours constituée par un régulateur, ou système de commande R, et par un processus asservi ou système réglé P, x désignant la grandeur d’entrée, de commande ou de référence, y la grandeur asservie, réglée ou de sortie, ε = x – y l’écart ou erreur et u la grandeur réglante ou correctrice. Si le régulateur est du type PID, son fonctionnement est décrit par une équation de la forme

soit encore, en dérivant par rapport au temps,

Si l’on représente par p le symbole de la différenciation, on a

Le rapport symbolique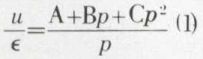

est appelé transmittance ou fonction de transfert du régulateur.

On définit de même la transmittance du processus P. De nombreux processus ont pour transmittance l’inverse d’un polynôme en p, par exemple pour un processus du troisième ordre :

En remplaçant ε par (x – y), les deux transmittances (1) et (2) permettent d’écrire

soit encore

D’où, enfin, la transmittance globale ou en boucle fermée

Ce système est stable si et seulement si toutes les racines du polynôme du dénominateur, appelé polynôme caractéristique, ont des parties réelles négatives. Mais il faut encore que ces parties réelles soient suffisamment négatives pour que le système possède un amortissement convenable.

Le critère de Naslin permet d’imposer aux coefficients du polynôme caractéristique des conditions suffisantes pour qu’il en soit ainsi. Pour un polynôme
a₀ + a₁p + a₂p² + ... + a_npⁿ,
ce critère consiste à imposer aux divers rapports

appelés rapports caractéristiques, d’être supérieurs ou égaux à une certaine valeur α, de l’ordre de 2. Ainsi, en égalant à 2 les trois rapports caractéristiques du dénominateur de la transmittance (3), il vient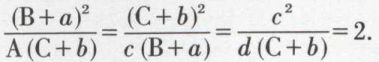

On peut ainsi calculer les valeurs des trois paramètres A, B et C de la loi de commande, connaissant les coefficients a, b, c, d de la transmittance du processus.

Analyse harmonique des systèmes asservis

Le point de vue de l’analyse harmonique est plus subtil. Considérons de nouveau la boucle d’asservissement définie plus haut. Si cette boucle est en régime d’auto-oscillation sinusoïdale avec x = 0, on a ε = – y, c’est-à-dire que y et ε oscillent à la même fréquence et avec la même amplitude, mais en opposition de phase. D’où l’idée d’étudier les propriétés de la boucle d’asservissement en régime permanent sinusoïdal (analyse harmonique). Si l’on excite par un signal u sinusoïdal de fréquence f le processus de transmittance P (p), le signal de sortie y est sinusoïdal de même fréquence f, mais son amplitude est différente de celle de u et, de plus, il est décalé, généralement en retard, par rapport à u ; on peut ainsi définir entre u et y un rapport d’amplitude, souvent appelé gain, et un déphasage, qui varient tous deux avec la fréquence f. Mathématiquement, le gain et le déphasage sont respectivement égaux au module et à l’argument de la fonction P  (jω), appelée transmittance isochrone, que l’on obtient à partir de P(p) en faisant p = jω, avec ω = 2πf et j² = – 1. On peut ainsi tracer une courbe de gain et une courbe de phase qui donnent respectivement les variations du gain et du déphasage en fonction de f ou de ω. On notera que ces courbes peuvent également être tracées expérimentalement, point par point, en mesurant le gain et le déphasage à diverses fréquences. On définit de même la transmittance isochrone R(jω) du régulateur.

Dans la boucle d’asservissement précitée, le gain et le déphasage subis par un signal sinusoïdal faisant le tour de la boucle sont donnés par la transmittance R(p)P(p), appelée transmittance en boucle ouverte, avec p = jω. Or, en régime d’oscillation auto-entretenue, le gain et le déphasage autour de la boucle sont égaux respectivement à l’unité et à – 180°. Si la boucle ouverte est stable, on peut en déduire que la boucle fermée l’est aussi, mais à condition que le déphasage de la boucle ouverte soit inférieur à 180°, en valeur absolue, à la fréquence pour laquelle le déphasage autour de la boucle est égal à l’unité. Cet énoncé constitue l’énoncé simplifié du célèbre critère de Nyquist. Il permet, lui aussi, de déterminer les paramètres du régulateur, connaissant ceux du processus conduit.

Extensions de l’analyse harmonique

Ces deux théories concernent les systèmes linéaires qui jouissent des deux propriétés de superposition et de proportionnalité des causes et des effets : l’effet de plusieurs causes agissant simultanément sur un système linéaire s’obtient en superposant les effets de ces mêmes causes agissant séparément. L’analyse harmonique a pu être généralisée à l’étude de certains types de systèmes non linéaires dits filtrés, dans lesquels on peut négliger les effets des harmoniques engendrés par un effet non linéaire tel que l’action d’un relais, la saturation d’un amplificateur ou un jeu mécanique. Le gain et le déphasage autour de la boucle sont alors fonction non seulement de la fréquence mais encore de l’amplitude. S’il existe une ou plusieurs paires de valeurs de la fréquence et de l’amplitude pour lesquelles le gain et le déphasage autour de la boucle sont respectivement égaux à l’unité et à – 180°, ces paires définissent des régimes d’auto-oscillation appelés oscillations limites, qui, pour être observables, doivent encore être stables ou convergents.