relativité (suite)

Einstein suppose en plus que le principe de relativité que nous avons énoncé est valable non seulement pour les lois de la mécanique, mais aussi pour toutes les lois physiques, à l’exception des lois de la gravitation, qui trouvent leur place naturelle dans la théorie de la relativité générale ; ainsi, les observateurs placés dans différents systèmes d’inertie doivent, par leurs expériences, arriver aux mêmes lois physiques. La notion d’espace absolu de Newton perd tout son sens. L’énorme simplification apportée par le principe de relativité doit, cependant, se payer, comme on va le voir, par un abandon des notions d’espace et de temps tirées du sens commun.

Invariance de la vitesse de la lumière, expérience de Michelson-Morley

L’invariance de la vitesse de la lumière c dans les différents systèmes de référence, qui est souvent considérée comme un postulat de la relativité restreinte, en est en fait une conséquence. En effet, les équations de Maxwell de l’électrodynamique, établies à partir de l’expérience et qui contiennent toutes les lois de l’électromagnétisme, renferment une quantité c qui est la vitesse des ondes électromagnétiques dans le vide, dans le système d’inertie de l’expérimentateur, mais qui peut aussi être déterminée indépendamment à partir des mesures purement électromagnétiques. D’après le principe de relativité, ces mesures doivent donner le même résultat quel que soit le système de référence : donc la vitesse de la lumière est invariante. Cela est en désaccord certain avec les concepts cinématiques usuels. Cependant, l’expérience célèbre de Michelson-Morley, en fait antérieure à l’énoncé de la relativité restreinte, puisqu’elle fut faite en 1881, puis refaite sous une forme moins critiquable en 1887, et d’autres expériences du même type ont fourni une confirmation éclatante de l’invariance de la vitesse de la lumière.

Cinématique relativiste

La constance de la vitesse de la lumière, impliquée par le principe de relativité, est, nous l’avons dit, en désaccord avec la cinématique et la mécanique classique (au moins pour les grandes vitesses), et nécessite l’introduction d’une nouvelle cinématique. On est, en particulier, obligé de faire intervenir de nouvelles propriétés de l’espace et du temps, décrites par la transformation de Lorentz, qui doit remplacer la transformation de Galilée, dont on a parlé plus haut. Voici comment on l’établit. Soit deux systèmes d’inertie S et S′ définis par des axes Ox, Oy, Oz et O′x′, O′y′, O′z′, parallèles, S′ étant animé de la vitesse v par rapport à S. Supposons, d’autre part, que les origines O et O′ de S et de S′ respectivement ont coïncidé au temps t = t′ = 0, t étant le temps dans S et t′ le temps dans S′. Soit un point A ; ses coordonnées sont x, y, z dans S et x′, y′, z′ dans S′ ; supposons qu’il envoie un éclair lumineux au moment où O et O′ sont confondus. Un observateur situé en O verra l’éclair après un temps t tel que – c²t² + x² + y² + z² = 0 ; de même, un observateur situé en O′ le verra après un temps t′ tel que
– c²t′² + x′² + y′² + z′² = 0
(c étant le même dans les deux systèmes).

On a donc entre les coordonnées spatiales et temporelles d’un point dans les systèmes S et S′ la relation
– c²dt² + x² + y² + z² = – c²dt′² + x′² + y′² + z′².
On en déduit les formules de Lorentz :

qui donnent les relations cherchées entre les coordonnées et le temps des deux systèmes d’inertie ; on remarque que, pour cette transformation de Lorentz se réduit à la transformation de Galilée.

Les vitesses ne se composent plus comme en cinématique newtonienne. C’est ainsi qu’un point ayant la vitesse de composantes u_x, u_y, u_z dans le système S aura par rapport au système S′ une vitesse de composantes :

expressions qui se réduisent aux expressions newtoniennes si

On peut déduire de la transformation de Lorentz d’intéressantes conclusions. L’une concerne le fait qu’une barre alignée selon la vitesse v et appartenant au système S′ apparaît plus courte à un observateur du système S qu’à un observateur du système S′. En effet, si et 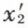sont les coordonnées des extrémités dans le système S′, la longueur dans ce système est 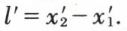Dans le système S, il est naturel de supposer que l’observateur mesure simultanément (c’est-à-dire au même temps t de son système S) la longueur de la barre dans S, qui sera donc l = x₂(t) – x₁(t) ; en utilisant la transformation de Lorentz, qui relie 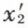à x₂(t) et à x₁(t), on trouve facilement que  : la barre paraît donc plus courte à un observateur de S, par rapport auquel elle est en mouvement, qu’à un observateur de S′.

Une autre conséquence de la cinématique relativiste est qu’une horloge en mouvement avec S′ paraît marcher plus lentement pour un observateur de S qu’une horloge identique au repos, et ce, quel que soit le sens de sa vitesse v : le retard est d’un facteur Il existe des vérifications expérimentales de cette « dilatation du temps » ; c’est ainsi que les mésons, particules instables et très rapides du rayonnement cosmique fabriquées dans la haute atmosphère à partir des particules cosmiques primaires, et dont la durée de vie est bien connue par des mesures au laboratoire sur des mésons au repos, parcourent dans l’atmosphère, avant de se désintégrer, une longueur plus grande que ne le laisserait prévoir cette durée de vie : c’est qu’en raison de leur vitesse leur durée de vie vue de la Terre est plus grande que celle qui est mesurée sur des mésons au repos. La « dilatation du temps » conduit aussi à un paradoxe apparent appelé souvent paradoxe du voyageur de Langevin. Elle prévoit qu’une horloge ayant été transportée à grande vitesse marquera à son retour au point de départ une heure antérieure à l’indication d’une horloge identique restée sur place (ou un jumeau ayant fait un tel voyage reviendra plus jeune que son frère). Cependant, ce paradoxe a fait l’objet de nombreuses discussions et ne peut être, en fait, résolu dans le cadre de la relativité restreinte, car celle-ci ne prévoit pas ce qui se passe pendant les phases d’accélération et de décélération qui existent nécessairement pendant le voyage. La relativité générale permet de traiter le problème complètement et montre que l’horloge en mouvement a mesuré après son voyage un temps plus petit que l’horloge fixe. L’expérience a été effectivement réalisée récemment en transportant en avion des étalons atomiques et en les comparant aux étalons restés au sol, et elle a donné une différence mesurée avec une faible précision relative, mais en accord avec la théorie. Cet accord n’est cependant pas une preuve sans ambiguïté de la validité de la relativité restreinte, ni d’ailleurs de la relativité générale.