linéaire (application) (suite)
3. Dans l’espace E des fonctions réelles continues sur ℝ, l’application u de E dans E qui à toute fonction f de E associe la fonction Φ de E telle que
est une application linéaire de E dans E en raison du caractère linéaire de l’intégrale définie
Propriétés des applications linéaires
Espace vectoriel des applications linéaires d’un espace vectoriel dans un autre
L’ensemble des applications linéaires d’un espace vectoriel E dans un espace vectoriel F, construits sur un même corps K, forme un espace vectoriel sur K.
Si f et g sont deux applications linéaires de E dans F, l’application s = f + g telle que
est l’application somme de f et de g. Cette application est linéaire, car
L’application αf telle que (αf) (u) = αf(u) avec α ∈ K est aussi linéaire, car
αf est l’application produit de f par le scalaire α. L’addition, dans l’ensemble des applications linéaires de E dans F, définie par s = f + g est associative et commutative comme l’addition dans F ; de plus, l’application nulle O définie par O(u) = O, ∀u ∈ E est telle que f + O = f, quelle que soit f ; enfin, – f + f = O, puisque (– f + f) (u) = f (u) – f (u) = O = O(u). L’application – f est l’application opposée de f. L’ensemble des applications linéaires de E dans F forme donc un groupe additif abélien.
De plus, la loi de composition externe qui à f associe αf confère à ce groupe abélien une structure d’espace vectoriel, tous les axiomes étant en effet vérifiés.
Anneau des endomorphismes linéaires
Les relations (1) et (2) montrent qu’une application linéaire de E dans F est un homomorphisme pour l’addition et la multiplication par un scalaire. Si E = F, l’application est un endomorphisme.
Si f : E → F et g : F → G sont linéaires, les trois espaces étant construits sur le même corps K, g ⃘ f application composée de f par g, est une application linéaire de E dans G. En effet,
ce qui met en évidence le caractère linéaire de g ⃘ f. De plus, la composition des applications est distributive par rapport à l’addition des applications (linéaires).
En effet, si f : E → F, g : E → F et h : F → G sont linéaires,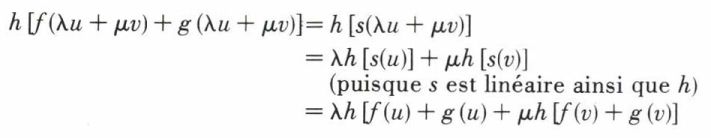

ce qui démontre la distributivité à gauche. On démontre la distributivité à droite de la même façon.
Si E = F = G, c’est-à-dire si on considère l’ensemble des endomorphismes linéaires de E dans E muni de l’addition des applications et de leur composition, on obtient un anneau. On a en effet un groupe additif abélien et une loi interne, la loi ⃘, associative et distributive par rapport à l’addition.
Automorphisme
Si f : E → F est linéaire et bijective, l’application inverse f –1 : F → E est aussi linéaire.
Si E = F, f : E → E, bijective et linéaire, est un homomorphisme bijectif, c’est-à-dire un automorphisme de E.
Noyau
C’est l’ensemble des vecteurs de E dont l’image par f est le vecteur nul de F (en anglais « kernel », noté « kerf », lu « ker de f »).
Si
Ce noyau n’est jamais vide ; en effet,
ce qui montre que O ∈ N. D’autre part, si u et v appartiennent à N, c’est-à-dire si
ce qui permet de vérifier que N est un sous-espace vectoriel de E.
On peut définir dans E une relation d’équivalence de la façon suivante : u ℛ v ⇔ u – v ∈ N ; on vérifie que ℛ est réflexive, symétrique et transitive. De plus, u – v = w ∈ N ⇔ u = v + w ⇔ f (u) = f (v), puisque f (w) = O, d’après la définition du noyau ; deux éléments u et v de N sont donc équivalents s’ils ont la même image par f. La classe d’équivalence d’un élément u de E est l’ensemble u + N. Si S est un sous-espace supplémentaire de N dans E, tout élément u de E se décompose de manière unique en une somme u = s + u, où s ∈ S et u ∈ N ; s est un représentant de la classe de u et il y a correspondance biunivoque en S et f (E), image de E par f. Si N se réduit à {O}, l’application f est une injection de E dans F ; c’est une bijection de E sur f (E).
Exemples.
1. Dans l’espace E des fonctions réelles continues, l’application
n’est pas injective ; la fonction  par exemple, appartient au noyau, car
par exemple, appartient au noyau, car
Le noyau de u est l’ensemble des fonctions de E périodiques et de période 1.
2. E est un espace vectoriel de dimension 3 sur ℝ ; une application linéaire f de E dans E est représentée par la matrice
c’est-à-dire que le vecteur v = xe1 + ye2 + ze3 de E est transformé en V = Xe1 + Ye2 + Ze3 de E tel que
On vérifie facilement que 2X – 2Y + Z = 0 ; autrement dit, l’image f (E) de E par f est le sous-espace de E de dimension 2, d’équation 2X – 2Y + Z = 0 (plan). Le noyau de f est l’ensemble des vecteurs v tels que – x + 2z = 0, y + 2z = 0, x + y = 0 ; c’est-à-dire des vecteurs tels que x = – y = 2z ; c’est un sous-espace vectoriel N de E de dimension 1 (droite de vecteur directeur 2, – 2, 1). L’application f n’est pas injective. Il y a bijection entre un sous-espace de dimension 2 de E, ne contenant pas le vecteur v1 = 2e1 – 2e2, + e3, et f (E), 2X – 2Y + Z = 0.
Rang d’une application linéaire en dimension finie
f : En → Fp est une application linéaire d’un espace vectoriel En de dimension n dans un espace vectoriel Fp de dimension p. Le rang de f est la dimension de f (En) ; il est inférieur ou égal à n et p. Comme f (En) est en correspondance biunivoque avec un sous-espace S supplémentaire du noyau N, si r est le rang de f et q la dimension du noyau, on a r + q = n. Dans l’exemple 2 ci-dessus, n = p = 3 ; q = 1, r = 2.
L’étude des applications linéaires en dimensions finies se fait à l’aide des matrices.
E. S.
➙ Application / Déterminant / Espace euclidien de dimension trois / Forme linéaire / Matrice / Vectoriel.






