Éd. 1971-1976

byzantin (Empire) (suite)

Icônes

Les icônes* peintes sur bois, à l’encaustique, avaient d’abord une valeur religieuse. Elles rendaient présents les intercesseurs auxquels la piété des fidèles aimait recourir. Elles étaient de la part des peintres l’objet d’un soin particulier ; elles aussi ont eu une longue et vaste influence : la Vierge dite « de Vladimir », peinte à Constantinople vers 1125, caresse de son visage celui de l’Enfant qui se courbe vers elle ; elle est à l’origine de bien des Vierges russes. Et partout les saints se ressemblent — saint Nicolas comme saint Jean Chrysostome.

Certaines images des manuscrits, on l’a vu, peintes à pleine page, ressemblent à des icônes ou reproduisent les grandes compositions de la peinture monumentale. Mais, souvent, l’illustration des textes sacrés ou des œuvres des Pères de l’Église a conduit à un enrichissement de l’iconographie et fourni des modèles aux fresquistes. L’esprit de toutes ces images saintes est le même, alors que chaque technique oblige sans cesse à des renouvellements.

Tissus

L’art du tissage* a connu aussi une grande fortune. Les sables d’Égypte nous ont conservé des lainages coptes, tissés et brodés, qui ont gardé une étonnante fraîcheur. À Constantinople, l’empereur s’était assuré le double monopole de la soie et de la pourpre. Le ver à soie avait été importé de Chine ; la pourpre était depuis longtemps connue, à partir de la Phénicie. La soie pourpre était un insigne impérial. Les motifs, souvent de tradition sassanide, stylisés et symétriques, ont une haute qualité décorative ; on en a retrouvé des exemples jusqu’en Occident, dans les tombes des princes et des saints.

Orfèvrerie, émaux

L’orfèvrerie, enfin, est extrêmement riche : les grands portaient des bijoux somptueux. Les trésors des églises et les musées conservent des calices d’argent et d’or ; les patènes, les croix d’autel, les croix processionnelles, les candélabres, les encensoirs, les éventails liturgiques, les reliquaires aussi, tous les objets nécessaires au culte ont servi de prétexte à des œuvres d’art minutieuses et éclatantes, souvent enrichies de pierreries. Les émaux concourent aussi à cette magnificence colorée. Leur technique, d’origine iranienne, qui enferme dans un cloisonnement d’or des pâtes étincelantes, a permis des réalisations à la fois délicates et somptueuses.

Tous ces accessoires de la vie princière, parce qu’ils étaient aussi ceux de la vie religieuse, ont atteint l’ensemble du peuple chrétien dans la splendeur des églises et des cérémonies. Ils appartenaient à la même recherche de somptuosité que les mosaïques à fond d’or. De nos jours encore, on retrouve à Ravenne, à Saint-Marc de Venise, à la chapelle Palatine de Palerme, à Dhafni, à Saint-Sauveur-in-Chora l’atmosphère de cette civilisation : le visiteur ébloui est comme enveloppé du chatoiement des ors et des couleurs, dans la lumière qui tombe des coupoles. Et il retrouve le sens d’un monde où rien n’était trop beau pour célébrer la majesté impériale ou la gloire du Seigneur.

ℂ

Corps des nombres complexes, c’est-à-dire des nombres de la forme a + bi, a et b étant réels et i le nombre imaginaire tel que i² = – 1.

Corps des complexes

Groupe additif abélien. Quels que soient z et z′ appartenant à ℂ, avec z = a + bi et z′ = a′ + b′i, z + z′ appartient aussi à ℂ, car
z + z′ = a + bi + a′ + b′i =
=(a + a′) + (b + b′)i = a″ + b″i et z + z′ = z′ + z ;
de plus, 0 ∈ ℂ, car 0 = 0 + 0i ; enfin, si z₁ = – a – bi, z + z₁ = 0 : z₁ est l’opposé de z ; comme l’addition des complexes ainsi définie est associative, ℂ, muni de cette opération, est un groupe additif commutatif ou abélien.

Groupe multiplicatif abélien. Si z = a + bi et z′ = a′ + b′i,
zz′ = (a + bi) (a′ + b′i) = aa′ – bb′ + i (ab′ + ba′), car i² = – 1.
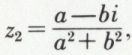Cette multiplication est associative, z(z′z″) = (zz′)z″, et commutative, zz′ = z′z ; de plus, 1 ∈ ℂ, car 1 = 1 + 0i ; enfin, si zz₂ = 1 ; z₂ est l’inverse de z, l’ensemble ℂ – {0}, muni de la multiplication ainsi définie, est un groupe multiplicatif abélien.

Distributivité de la multiplication par rapport à l’addition. On peut vérifier que z(z′ + z″) = zz′ + zz″, quels que soient les nombres complexes z, z′ et z″. Ces propriétés confèrent à l’ensemble ℂ, muni de l’addition et de la multiplication, une structure de corps commutatif. Le sous-ensemble de ℂ constitué par les nombres z de la forme z = a + 0i = a est l’ensemble des nombres réels. Le sous-ensemble de ℂ constitué par les nombres de la forme z = 0 + bi = bi est l’ensemble des nombres imaginaires purs ; le nombre i en fait partie. Pour calculer sur les nombres complexes, on utilise les règles de calcul valables dans le corps des nombres réels, sans oublier de remplacer i² par – 1, i³ = i₂ × i par – i et i⁴ = (i²)² par 1.

Représentation géométrique d’un nombre complexe

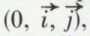À tout nombre complexe z = a + bi, on associe, dans le plan rapporté à un repère orthonormé le point M, unique, de coordonnées a et b ; M s’appelle l’image de z, et z l’affixe de M. Inversement, à tout point P (α, β) correspond le nombre u = α + iβ, unique.

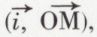Le module de z, noté |z|, est la longueur du segment OM ;

L’argument de z, noté arg z, est la mesure de l’angle de vecteurs connue à 2kπ près, en radians ;
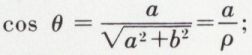
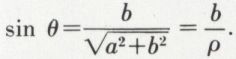L’argument θ est complètement défini par les égalités On peut alors passer de la forme algébrique a + bi à la forme trigonométrique de z, z = ρ (cos θ + i sin θ). Deux nombres complexes
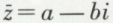z = a + bi = ρ (cos θ + i sin θ) et z′ = a′ + b′i = ρ′ (cos θ′ + i sin θ′)
sont égaux s’ils ont même image ou si a = a′ et b = b′, ou ρ = ρ′ et θ = θ′ + 2kπ. Deux nombres complexes z = a + bi et z′ = a′ + b′i sont imaginaires conjugués si leurs images sont symétriques par rapport à Ox ; alors a′ = a et b′ = – b ; d’où z′ = a – bi ; on note (on lit « z barre ») ; réel et réel positif ; de plus,