quadratique sur un espace vectoriel E sur un corps K (forme) (suite)
Le noyau de la forme quadratique Q est l’ensemble des x de E tels que ∀y ∈ E,  c’est donc l’orthogonal de E. Quand l’espace vectoriel E est de dimension finie, une forme quadratique est non dégénérée si et seulement si son noyau se réduit à {0}. Pour qu’il en soit ainsi, il faut et il suffit que la forme bilinéaire B soit elle-même non dégénérée, c’est-à-dire que son rang soit maximal, égal donc à n si E est un espace vectoriel de dimension n. Le rang d’une forme quadratique Q est celui de sa forme polaire B. On le détermine, dans une base donnée, à l’aide du déterminant de la matrice symétrique M de la forme quadratique Q ou de sa forme polaire B ; dét M s’appelle le discriminant de Q et de B. Ce discriminant n’est pas invariant dans un changement de base, mais sa nullité ou sa non-nullité sont invariantes. Ainsi, Q et B sont dégénérées, ou non, suivant que dét M = 0 ou dét M ≠ 0, ce qui fournit un moyen pratique de détermination de la dégénérescence.
c’est donc l’orthogonal de E. Quand l’espace vectoriel E est de dimension finie, une forme quadratique est non dégénérée si et seulement si son noyau se réduit à {0}. Pour qu’il en soit ainsi, il faut et il suffit que la forme bilinéaire B soit elle-même non dégénérée, c’est-à-dire que son rang soit maximal, égal donc à n si E est un espace vectoriel de dimension n. Le rang d’une forme quadratique Q est celui de sa forme polaire B. On le détermine, dans une base donnée, à l’aide du déterminant de la matrice symétrique M de la forme quadratique Q ou de sa forme polaire B ; dét M s’appelle le discriminant de Q et de B. Ce discriminant n’est pas invariant dans un changement de base, mais sa nullité ou sa non-nullité sont invariantes. Ainsi, Q et B sont dégénérées, ou non, suivant que dét M = 0 ou dét M ≠ 0, ce qui fournit un moyen pratique de détermination de la dégénérescence.
La base (e1, e2, ..., en) de l’espace E est dite orthogonale pour Q si B(ei, ej) = 0 pour i ≠ j ; elle est dite orthonormale si B(ei, ej) = δij (δij est le symbole de Kronecker ; δij = 0 pour i ≠ j et δij = 1 pour i = j) ; i et j ∈ {1, 2, ..., n}. Pour toute forme quadratique Q sur un espace vectoriel E de dimension finie n, il existe une base de E orthonormale pour Q ; il existe aussi une base de E telle que la matrice de Q dans cette base soit diagonale. Dans une telle base, on a donc 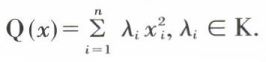
Dans une base orthogonale pour Q, le rang de Q est le nombre d’éléments non nuls parmi les éléments λi de la matrice de Q.
Classification des formes quadratiques à coefficients réels
Deux formes quadratiques Q1 et Q2 sur l’espace vectoriel E sont dites équivalentes s’il existe deux bases (e1, e2, ..., en) et (f1, f2, ..., fn) de E telles que la matrice de Q1 dans  soit la même que la matrice de Q2 dans
soit la même que la matrice de Q2 dans  Toute forme quadratique Q de rang r sur ℝn est équivalente à une forme du type
Toute forme quadratique Q de rang r sur ℝn est équivalente à une forme du type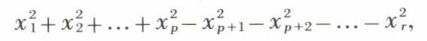
p ∈ ℕ et ne dépend que de Q ; 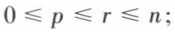 ce résultat est connu sous le nom de loi d’inertie de Sylvester.
ce résultat est connu sous le nom de loi d’inertie de Sylvester.
Ce théorème signifie que, si l’on passe d’une forme Q à une forme équivalente Q1, puis à une autre forme équivalente Q2, on obtient le même nombre de signes + et le même nombre de signes –. Le couple (p, q), p désignant le nombre de carrés précédés du signe + et q le nombre de carrés précédés du signe –, est appelé la signature ou le type de la forme quadratique Q. Une forme quadratique sur ℝn est dite définie positive si elle est de type (n, 0), définie négative si elle est de type (0, n) ; elle est dite positive si elle est de rang r et de type (r, 0), négative si elle est de rang r et de type (0, r).
Méthode pratique de décomposition en carrés d’une forme quadratique à coefficients réels
On utilise un procédé dû à Gauss et qui permet de mettre une forme quadratique sous la forme  les éléments ui étant des formes linéaires indépendantes. La signature est alors en évidence : p est le nombre des formes précédées du signe + et q celui des formes précédées du signe –. La pratique de la décomposition est la suivante.
les éléments ui étant des formes linéaires indépendantes. La signature est alors en évidence : p est le nombre des formes précédées du signe + et q celui des formes précédées du signe –. La pratique de la décomposition est la suivante.
1. La forme Q contient au moins un terme carré, soit
d’où
On recommence la décomposition en carrés sur la forme
en utilisant un terme carré, s’il y en a un, ou l’un des termes rectangles s’il n’y a plus de termes carrés.
2. La forme quadratique Q ne contient que des termes rectangles, soit
Q(x) = ax1x2 + A(x3, ..., xn)x1 + B(x3, ..., xn)x2 + C(x3, ..., xn).
On a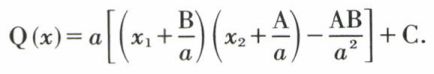
L’identité  donne alors
donne alors
d’où
et l’on poursuit la décomposition de la forme quadrique  en utilisant un terme carré ou un terme rectangle suivant que l’on se trouve dans le cas 1 ou 2.
en utilisant un terme carré ou un terme rectangle suivant que l’on se trouve dans le cas 1 ou 2.
Exemples de décomposition de formes quadratiques en carrés.
• Décomposer sur ℝ3 la forme quadratique
f(x, y, z) ≡ x2 + y2 + z2 – 3yz – zx – xy ;
on a successivement :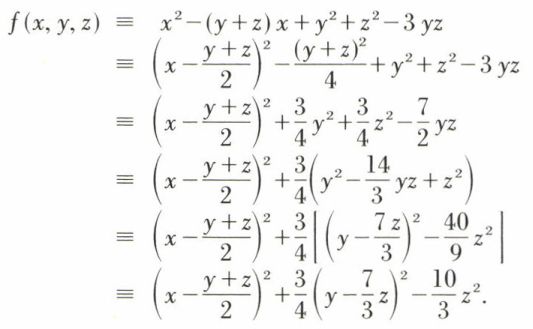
La signature de f(x, y, z) est (2, 1) ; les trois formes linéaires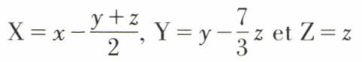
sont linéairement indépendantes, puisqu’on peut donner à Z la valeur arbitraire λ (pour z = λ) ; ayant ainsi disposé de z, on peut donner à Y la valeur arbitraire  on peut enfin donner à X la valeur arbitraire ν, puisqu’on peut encore disposer de x dans
on peut enfin donner à X la valeur arbitraire ν, puisqu’on peut encore disposer de x dans 
• Décomposer sur ℝ3 la forme quadratique
La forme f(x, y, z) est du type (1, 2). Il est évident, sur cet exemple, que l’on arrive toujours au même couple (1, 2), puisque xy + yz + zx est symétrique en x, y et z.
L’étude des formes quadratiques conduit à celle des espaces euclidiens et aussi à la classification des coniques et des quadriques.
E. S.
➙ Conique / Espace euclidien de dimension trois / Forme linéaire / Quadrique / Vectoriel.
H. Blanchard et C. Forest, Traité de mathématiques (Hachette, 1966-1970 ; 3 vol.). / J. Lelong-Ferrand et J. M. Arnaudiès, Cours de mathématiques, t. I : Algèbre (Dunod, 1971).





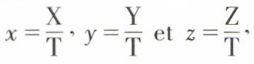 une quadrique (S) a comme équation
une quadrique (S) a comme équation
