sphère

Surface fermée dont tous les points sont à la même distance (rayon) d'un point intérieur (centre) ; solide limité par la surface précédente.

MATHÉMATIQUES

Dans l'espace affine E₃ de dimension 3, l'aire d'une sphère de rayon r est 4πr² et son volume intérieur .

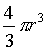Dans un repère orthonormé de E₃, une sphère de rayon r et de centre A(a, b, c) a pour équations paramétriques :
x = r. cos u. sin v + a
y = r. sin u. sin v + b
z = r. cos v + c
où u ∈ [0,2π] et v ∈ [0, π].

Elle a pour équation cartésienne :
x² + y² + z² − 2 (ax + by + cz) + (a² + b² + c² − r²) = 0
où M (x, y, z) est un point variable de S.

L'intersection d'une sphère et d'un plan est un cercle.