loi de Laplace-Gauss ou loi de Gauss ou loi normale
Loi d'une variable aléatoire absolument continue X dont la densité de probabilité est :
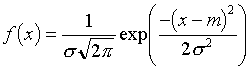
m et σ étant deux nombres réels, σ strictement positif.
La loi de Laplace-Gauss centrée réduite est un cas particulier d'une loi de Laplace-Gauss où m = 0 et σ = 1. La loi de Laplace-Gauss est d'une grande importance en probabilité. De nombreux phénomènes peuvent en effet se rattacher à son modèle et on peut approximer la loi binomiale et la loi de Poisson par la loi de Laplace-Gauss. L'espérance mathématique d'une variable de Laplace-Gauss est m, sa variance σ2 et son écart-type σ.




