intégrale

Limite, lorsqu'elle existe, de sommes d'un nombre indéfiniment croissant d'éléments indéfiniment petits construits en divisant indéfiniment le domaine de définition d'une fonction.

MATHÉMATIQUES

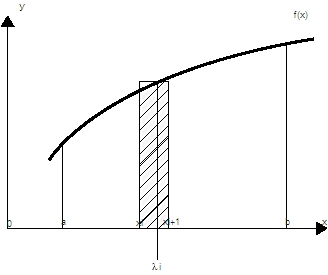
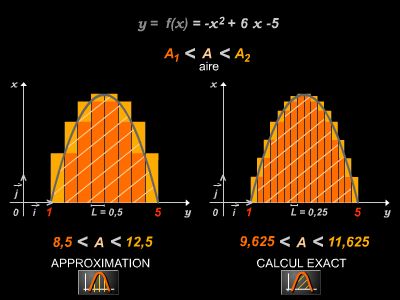
Pour construire, par exemple, l'intégrale d'une fonction numérique f(x) définie et bornée sur un intervalle [a, b], on divise celui-ci en un nombre N d'intervalles [x_i, x_i+1]. On prend une valeur λ_i quelconque dans l'intervalle [x_i, x_i+1] et on forme le produit p_i = f(λ_i)(x_i+1 − x_i), représenté géométriquement par l'aire du rectangle hachuré (voir figure). On fait la somme S_N de tous ces produits p_i. Si, lorsque N tend vers l'infini et (x_i+1 − x_i) tend vers 0, S_N a une limite S, celle-ci est l'intégrale de f(x) sur [a, b] notée 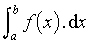, et est représentée, si f est toujours positive, par l'aire de la surface comprise entre le graphe de f(x), l'axe O x et les verticales en a et b. La fonction f(x) est alors dite intégrable. La même construction est valable pour les intégrales doubles ou triples, en remplaçant les intervalles [x_i, x_i+1] de ℝ par des domaines élémentaires de ℝ² ou de ℝ³.

Le calcul des intégrales a une importance capitale en mathématiques et dans les sciences et les techniques. Pour calculer les intégrales simples on se sert souvent de la propriété suivante : si F est une primitive de f, 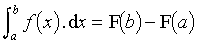. Cette relation est valable si f est définie et continue sur [a, b]. Si on ne connaît pas de primitive, on utilise des intégrateurs ou des méthodes numériques aujourd'hui facilement mises en œuvre sur ordinateur.