conique

Intersection d'un cône du second degré avec un plan ne contenant pas le sommet.
Classification des coniques
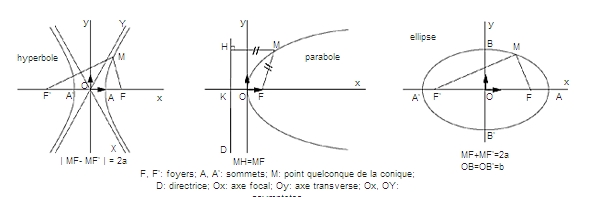
Les coniques ont une équation cartésienne de la forme
ax2 + 2bxy + cy2 + dx + ey + f = 0,
a, b, c non tous nuls.
Les directions asymptotiques de la conique ont pour coefficients directeurs les solutions m de l'équation cm2 + 2bm + a = 0.
– b2−ac > 0. La courbe a deux directions asymptotiques distinctes ; c'est une hyperbole si elle n'est pas décomposée en deux droites sécantes.
– b2−ac = 0. La courbe a deux directions asymptotiques confondues ; c'est une parabole si elle n'est pas décomposée en deux droites parallèles.
– b2−ac < 0. La courbe n'a pas de branche infinie ; c'est une ellipse si ce n'est pas l'ensemble vide.
Le centre de symétrie n'existe que pour les ellipses et les hyperboles (b2−ac = 0) et est donné par les équations ax + by + d = 0 et bx + cy + e = 0.
Équations réduites
Par un changement de repère convenable, on peut prendre pour axes de coordonnées les axes de symétrie des ellipses et hyperboles ; les équations deviennent :
– pour l'ellipse
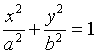 ;
;
– pour l'hyperbole
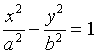 ; dont les asymptotes ont pour équation
; dont les asymptotes ont pour équation
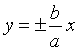
;
– pour la parabole y2 = 2px.
Équations paramétriques :
ellipse
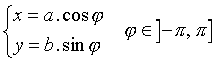
hyperbole
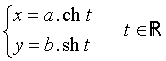
En prenant comme axes ses asymptotes, l'hyperbole a une équation de la forme XY = k et réciproquement.




