ℂ
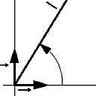
Symbole représentant le corps des nombres complexes. (ℂ est l'ensemble dont les éléments sont de la forme générale a + ib, où a et b sont des réels et i tel que i2 = − 1.)
Tout élément z de ℂ s'écrit de manière unique z = x + iy ; x est appelé la partie réelle de z [notée
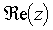] et y la partie imaginaire de z [notée
]. À tout nombre complexe z = x + iy, on associe, dans le plan rapporté à un repère orthonormé
, le point M de coordonnées (x,y) ; M s'appelle l'image de z et z est l'affixe de M. Inversement, à M′(x′, y′) du plan correspond le nombre z′ = x′ + iy′ appartenant à ℂ. Le module de z, noté
, est la longueur OM :
, donc
. L'argument de z, noté arg z, est la mesure de l'angle des vecteurs
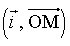, connue à 2kπ près en radians. Si on note θ cet angle, il est déterminé par :
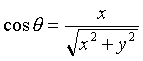, et
;
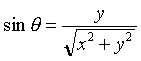z s'écrit alors :
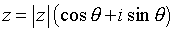, ce qui est la forme trigonométrique de ce nombre. Pour z = x +iy, on appelle conjugué de z le nombre
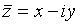. Si z est non nul, son inverse s'écrit
. La formule de Moivre permet de déterminer simplement les puissances d'un nombre complexe écrit sous forme trigonométrique :
.
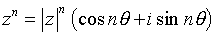
