équation différentielle

Équation de la forme 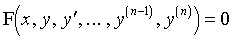, où F est une fonction de n + 2 variables réelles (ou complexes). [n est l'ordre de l'équation. ψ est solution de cette équation si ψ est n fois dérivable sur un intervalle I et si x ↦ F x,ψ(x), …, ψ⁽ⁿ⁾(x) est définie sur I et coïncide sur I avec la fonction nulle.]

MATHÉMATIQUES

Équations différentielles linéaires du premier ordre

Elles sont de la forme : y′ + a(x).y = g(x). On étudie d'abord l'équation linéaire sans second membre, encore appelée équation linéaire homogène associée, y′ + a(x).y = 0, dont les solutions sont ψ_λ : x↦λ. e^−A(x), où A est une primitive de a et λ une constante réelle quelconque. Toutes les solutions de l'équation avec second membre sont obtenues en ajoutant à l'une d'entre elles toutes les solutions ψ_λ.

Méthode de la variation de la constante. Si y₁ est solution de l'équation homogène associée, pour que y = u.y₁ soit solution, on doit avoir

u′ = g/y₁ et u(x) = G(x) + C,

où G est une primitive de g/y₁ ; la solution générale sera la famille y = G.y₁ + C.y₁.

On se ramène à de telles équations différentielles dans le cas des équations de Bernoulli et de Riccati.

Équations différentielles linéaires du second ordre à coefficients constants

Sans second membre, elles s'écrivent

. On étudie l'équation caractéristique

a.r² + b.r + c = 0.(1).

1^er cas. b² − 4ac ≠ 0 :
si r₁ et r₂ sont deux solutions réelles de (1), les solutions de l'équation différentielle sont alors

, (λ₁, λ₂)∈ℝ² ;

si r₁ et r₂ sont deux solutions complexes conjuguées de (1), r₁ = α + iβ et r₂ = α − iβ, les solutions sont alors y = e^αx (μ₁. cos βx + μ₂. sin βx), (μ₁, μ₂)∈ℝ².2^e cas. b² − 4ac = 0 : si r est la solution double de (1), les solutions de l'équation différentielle sont y = e^r.x(λx + μ), avec λ et μ constantes réelles.

Avec second membre, elles sont de la forme

.

Si g est une fonction polynôme, on peut obtenir une solution particulière par identification, sous la forme d'un polynôme de même degré que g, et de là, à l'aide de l'équation sans second membre, on obtient la famille des solutions générales.