déterminant d'une matrice carrée M = (αij) d'ordre n sur un corps K
Déterminant des n vecteurs colonnes ou des n vecteurs lignes dans la base canonique de Kn.
On note :
Un tel déterminant est dit d'ordre n. On peut développer un déterminant suivant la i èmeligne ou la j ème colonne : si on note Mij la matrice obtenue en enlevant la i ème ligne et la j ème colonne, alors
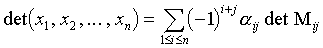
(par rapport à la i ème ligne). On appelle (−1)i + j det Mij cofacteur de αij et det Mij mineur associé à αij. Lorsque le déterminant de n vecteurs est non nul, les vecteurs sont alors linéairement indépendants (et réciproquement). Lorsque le déterminant d'un endomorphisme est non nul, l'endomorphisme est alors inversible (et réciproquement).