ℚ
Symbole de l'ensemble des nombres rationnels ou corps des fractions de l'anneau ℤ des entiers relatifs. (Les éléments de ℚ sont les nombres égaux au quotient d'un entier relatif a par un entier relatif non nul b, noté à l'aide des notations fractionnaires
 .)
.)
La construction mathématique de l'ensemble ℚ se fait à partir de l'étude de la relation d'équivalence R définie sur ℤ × ℤ par (a, b) R (a′, b′) si et seulement si ab′ = ba′. L'ensemble quotient ℤ × ℤ*/R est l'ensemble ℚ ; chaque classe d'équivalence est appelée un rationnel et a une infinité de représentants. Si (a, b) est un représentant de la classe, traditionnellement la classe de (a, b) est représentée par la notation fractionnaire
 et, par abus de langage, cette classe est parfois appelée fraction, d'où le nom de corps des fractions de ℤ. Parmi les différents représentants d'un rationnel, il est souvent intéressant de prendre celui d'une fraction irréductible. Dans la pratique, un rationnel est utilisé en tant que quotient de deux entiers. Les règles de calcul des quotients s'appliquent donc aux rationnels. Muni de l'addition et de la multiplication
et, par abus de langage, cette classe est parfois appelée fraction, d'où le nom de corps des fractions de ℤ. Parmi les différents représentants d'un rationnel, il est souvent intéressant de prendre celui d'une fraction irréductible. Dans la pratique, un rationnel est utilisé en tant que quotient de deux entiers. Les règles de calcul des quotients s'appliquent donc aux rationnels. Muni de l'addition et de la multiplication
(
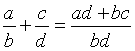 ,
,
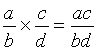 , a ∈ ℤ, b ∈ ℤ*, c ∈ ℤ, d ∈ ℤ*)
, a ∈ ℤ, b ∈ ℤ*, c ∈ ℤ, d ∈ ℤ*)
et de la relation d'ordre ≤, ℚ est un corps totalement ordonné, archimédien, dense dans lui-même (pour tous rationnels x et y tels que x < y, il existe un rationnel z tel que x < z < y), dense dans ℝ (pour tous réels a et b tels que a < b, il existe une infinité de rationnels appartenant à l'intervalle ]a, b[). ℚ est un sous-corps du corps des réels ℝ.



