mesure

Rapport numérique d'une grandeur à une autre grandeur de même nature prise comme unité ; repérage de la position d'une grandeur dite repérable dans une échelle admise par convention, même si l'on ne sait pas définir le rapport à une unité.

MÉTROLOGIE

Une mesure s'effectue à l'aide d'un instrument de comparaison et d'une série d'objets étalonnés, réalisant une série de rapports connus à l'unité (balance et masses marquées, boîtes de résistances, etc.), ou avec un instrument à échelle graduée et étalonnée (pied à coulisse, balance automatique, voltmètre, etc.). Les causes d'erreur étant multiples, on utilise, pour en réduire l'importance, des méthodes appropriées (double pesée) et on applique des corrections de compensation (correction d'étalonnage, de température, etc.). Les erreurs résiduelles et aléatoires sont étudiées par une approche statistique ; on les caractérise par une marge d'incertitude. (→ métrologie.)

L'incertitude des mesures

Dans une série de mesures, la dispersion, c'est-à-dire les différences constatées d'une mesure à l'autre, a des causes variables. Les erreurs des mesures physiques sont principalement dues : 1. aux fautes de l'observateur : mauvaise lecture, etc. ; 2. aux erreurs personnelles, par exemple retard dans le déclenchement d'un chronomètre ; 3. aux erreurs stochastiques, toujours présentes, qui proviennent de la limitation des instruments, du mouvement brownien, de l'interférence de sources ou du milieu extérieurs, d'effets quantiques, etc. ; 4. aux erreurs systématiques, qui proviennent d'erreurs de calibration ou d'effets négligés. Les erreurs systématiques sont les plus graves et souvent les plus difficiles à repérer. Les méthodes de la statistique sont appliquées aux erreurs, en particulier pour déterminer l'erreur standard du résultat d'une expérience.

Les erreurs systématiques

Certaines provoquent un écart toujours orienté dans le même sens (positif ou négatif) par rapport à la valeur de référence : c'est le cas des mauvais réglages de l'étalonnage ou du zéro de l'appareil de mesure. Ainsi, si l'on utilise un pèse-personne qui indique 1 kg à vide, le poids sera erroné à chaque pesée, et toujours surestimé. Ces erreurs, dites systématiques, peuvent généralement être corrigées (par un réglage du zéro, par exemple).

Les erreurs aléatoires

Après correction, une dispersion peut demeurer : en se pesant plusieurs fois de suite, on observe parfois quelques variations, car de petits écarts se sont produits dans un sens ou dans un autre sans qu'on puisse en connaître les causes. Ces petits écarts produisent la dispersion. On les désigne par l'expression d'erreurs aléatoires, expression qui indique qu'une certaine part de hasard est liée au phénomène de dispersion.

La prise en compte des erreurs dans la mesure

La distinction entre erreur systématique et erreur aléatoire est souvent difficile à établir, au point qu'un procédé courant consiste à rendre aléatoires des erreurs en général classées comme systématiques, mais qu'on ne parvient pas à corriger. Il s'agit de recourir à un grand nombre d'appareils de mesure afin que les variations enregistrées puissent être attribuées non plus aux défauts éventuels d'un seul appareil mais aux différences aléatoires existant d'un appareil à l'autre.

Pour comprendre pourquoi les physiciens utilisent la notion de hasard dans la description de ce phénomène, il faut imaginer ce qui se passerait si l'on faisait une infinité de mesures. Cela correspond en statistique à une population dont on extrait un échantillon de n mesures. Les valeurs composant la population dite parente se regroupent autour d'une valeur centrale, avec quelques valeurs qui s'en écartent. Cela apparaît si l'on représente les résultats à l'aide d'un histogramme, qu'il s'agisse d'une infinité de pesées d'une même personne, de mesures d'une intensité avec une infinité d'ampèremètres, ou de toute autre série de mesures. La figure obtenue est proche d'un histogramme symétrique : elle correspond à la répartition statistique de Gauss illustrant le théorème central limite, ou de la limite centrée, qui se vérifie moyennant quelques conditions quant aux modalités de réalisation des mesures (elles doivent en particulier être indépendantes les unes des autres).

L'élimination la plus complète possible des erreurs systématiques a pour but d'améliorer la qualité du résultat, de le rendre le plus exact possible. Tenter de se dégager des erreurs aléatoires revient à améliorer une autre qualité du résultat de la mesure, la précision.

Le hasard des mesures

Il existe des phénomènes physiques pour lesquels il est difficile d'établir des prédictions, car leur nature fait que la moindre variation des conditions initiales modifie le résultat de l'expérience. C'est le cas d'un obus qui semble lancé toujours de la même façon et qui ne tombe jamais exactement au même endroit, ou d'une bille lancée sur un obstacle cylindrique (un clou, par exemple).

Le physicien est confronté à des phénomènes qui, bien qu'obéissant à des lois déterministes, ont des résultats imprévisibles : il dit alors que le résultat est aléatoire et que c'est le hasard déterministe qui gouverne ces phénomènes ; les statistiques permettent des prévisions non pas de chaque expérience mais, globalement, d'un ensemble d'expériences.

L'outil statistique et la précision

Les théorèmes de statistique démontrent que plusieurs mesures permettent de renforcer la qualité des informations recueillies.

Ces théorèmes exploitent le résultat selon lequel l'histogramme de la population des mesures correspond à la représentation graphique de la loi de probabilité de Gauss, qui est une fonction mathématique P(x), normée (c'est-à-dire dont l'aire comprise entre la courbe et l'axe des abscisses est égale à 1), symétrique par rapport à une valeur centrale μ, et définie par la quantité σ (σ² est la variance de la distribution).

Le point d'inflexion est le point de la courbe où la courbure change de sens ; mathématiquement, la dérivée seconde s'annule en ce point.

Des tables donnent la valeur de ces fonctions pour toute valeur de x. D'autres tables permettent de calculer toute aire comprise entre la courbe de Gauss, l'axe des abscisses et l'axe des parallèles à l'axe des ordonnées. Ainsi, les résultats numériques suivants sont souvent utilisés en théorie de la mesure sous deux formes : la valeur des aires et l'interprétation en termes de probabilités.

En réalité, on ne fait jamais une infinité de mesures, mais l'on étudie un échantillon de n mesures. On démontre que le meilleur représentant d'une telle série, ce que les statisticiens appellent le meilleur estimateur de la valeur centrale de la population, est sa moyenne, x₀. De même, le meilleur estimateur de la variance de la population parente correspond à une valeur s, telle que (avec n > 1) :

La moyenne x₀ et l'écart moyen quadratique s_n–1 (noté souvent s) sont donnés par les calculatrices munies des fonctions statistiques. Ces deux valeurs étant obtenues, on peut calculer un intervalle dans lequel le centre μ de la population parente a 95 % de chances de se trouver (ou 68 % ou tout autre pourcentage donné par les tables numériques). Par exemple, pour plus de 20 mesures, la valeur μ a :
95 % de chances de vérifier

68 % de chances de vérifier

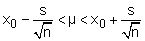
Les coefficients 1,96 et 1 multipliant s doivent être remplacés par d'autres coefficients si n est inférieur à une valeur que l'on prend environ égale à 20 : par exemple, 1,96 doit être remplacé par 2,26 si on ne dispose que de 10 mesures, et par 2,77 si on ne dispose que de 5 mesures.

Améliorer le résultat d'un mesurage

La qualité d'un mesurage dépend de deux facteurs : la précision, qui relève des techniques de calcul employées, et l'exactitude, qui est déterminée par les conditions dans lesquelles s'effectue la mesure. L'outil statistique permet d'améliorer la précision. Les formules montrent que celle-ci dépend de deux facteurs, la variance des n mesures réalisées et le nombre n de mesures : plus n est grand, plus les effets des erreurs aléatoires sont réduits, plus la précision est améliorée. Ainsi, si on passe d'une série de n mesures à une série de 100 n mesures, on divise par 10 l'amplitude de l'intervalle de confiance correspondant à un même taux de confiance. De fait, il est tout à fait inutile de poursuivre trop loin la recherche de précision si on n'a pas les moyens d'améliorer de la même façon l'exactitude. Ainsi, il serait absurde de se peser 100 fois de suite sur un pèse-personne qui ne dispose pas d'un réglage à vide fiable. L'exactitude s'améliore en réduisant au minimum les erreurs systématiques, ce qui suppose une réflexion sur le phénomène lui-même et sur la méthode de mesure. Les histogrammes associés (figure ci-dessous) présentent l'une et/ou l'autre qualité. Multiplier les mesures dans le premier cas n'apporterait aucune information supplémentaire, étant donné l'inexactitude liée aux conditions du mesurage.

La transmission des incertitudes

Le problème suivant se pose fréquemment lors d'opérations de mesurage : si une grandeur z est fonction d'autres grandeurs, par exemple x et y, et si x et y sont elles-mêmes entachées d'incertitude, z, qu'on peut écrire alors sous la forme z = f(x, y), se trouve aussi entachée d'incertitude. Il faut savoir déduire Δz de Δx et Δy. C'est ainsi que la vitesse de rotation d'un moteur synchrone est proportionnelle à la fréquence n du courant alternatif qui l'alimente (ω = 2π n). S'il s'agit du courant du secteur, dont la fréquence de 50 Hz est garantie par EDF à 1 Hz près, la vitesse de rotation du moteur sera garantie à 2π rad/s, soit 6,28 rad/s. Cette incertitude se transmet également à d'autres quantités, comme la vitesse linéaire de l'extrémité d'un bras entraîné par l'axe du moteur. Dans cet exemple, la vitesse linéaire de l'extrémité d'un bras de 50 cm est constante à 3,14 m/s près.

Le problème de la transmission des incertitudes est traité mathématiquement : on considère en effet que celles-ci sont de petites variations autour de la valeur de référence, et on utilise le calcul différentiel. On peut alors écrire, par exemple pour deux variables :

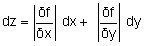
(les dérivées partielles sont calculées pour les valeurs moyennes de x et y mesurées).

Cette formule montre que chacune des variables contribue à l'incertitude sur z. Elle se développe différemment suivant la connaissance que l'on a des incertitudes sur x et sur y.

– Dans un premier cas, on connaît les incertitudes Δx et Δy. On a :

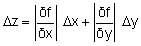
Δz apparaît ainsi comme la somme des contributions des incertitudes sur x et sur y.

On peut l'appliquer au cas du moteur évoqué plus haut, où v est la vitesse linéaire du bras ; v = 2π nl (l étant la longueur du bras). EDF garantit Δn = 1 Hz, et la longueur du bras peut être connue à 1 mm près, donc Δl = 0,001 m.

Que vaut Δv pour le moteur ?

Avec les valeurs numériques données ci-dessus, on obtient : Δv = (3,14 + 0,314) m/s. On se rend compte que l'incertitude due à la fréquence est 10 fois plus grande que celle due à la longueur : les contributions sont très différentes.

– Un autre cas est celui où l'on a réalisé plusieurs mesures de x et y. On calcule alors l'intervalle de confiance pour x et pour y (soit Ix et Iy), et on peut écrire une formule qui donne une bonne évaluation de l'intervalle de confiance pour z (soit Iz) moyennant quelques conditions :

Comme précédemment, chacune des variables contribue à l'intervalle de confiance de la fonction.

Par exemple, si 20 étudiants recherchent la valeur d'une même résistance R en mesurant le courant J et la tension V, ils peuvent chacun à leur tour affirmer :
J a 95 % de chances de se trouver dans l'intervalle I_J ;
V a 95 % de chances de se trouver dans l'intervalle I_V ;
R a donc 95 % de chances de se trouver dans l'intervalle (I_J² + I_V²)^1/2.

On notera que ces calculs sont valables dans le cas où les grandeurs x et y sont indépendantes ; sinon, la transmission des erreurs est plus complexe.