matrice

Famille (α_ij) d'éléments d'un corps K, (i, j) ∈ { 1, …, n } × { 1, …, p}, n et p étant deux naturels, habituellement présenté sous la forme d'un tableau rectangulaire à n lignes et p colonnes [matrice de type (n, p)].

MATHÉMATIQUES

Si M = (α_ij) est une matrice de type (n, p), l'élément α_ij est à l'intersection de la i^ième ligne et de la j^ième colonne. Les éléments d'une même ligne forment un vecteur ligne ; les éléments d'une même colonne forment un vecteur colonne.

Si n = 1, la matrice est dite matrice ligne ;
si p = 1, la matrice est dite matrice colonne ;
si n = p, la matrice est dite matrice carrée d'ordre n.
Les éléments α_ii d'une matrice carrée, appelés éléments diagonaux, forment la diagonale principale de la matrice. Si les éléments situés symétriquement par rapport à cette diagonale sont égaux (α_ij = α_ji), la matrice est dite symétrique.

L'ensemble des matrices de type (n, p) sur un corps K se note M_{n, p}(K). L'ensemble des matrices carrées d'ordre n sur un corps K se note M_n(K).

Structure de l'ensemble M_{n, p}(K)

L'addition de deux matrices M = (α_ij) et M′ = (α′_ij) est définie par M + M′ = (β_ij) avec β_ij = α_ij + α′_ij. La multiplication externe d'une matrice M = (α_ij) par un scalaire λ est définie par λM = (β_ij), avec β_ij = λα_ij. Muni de ces deux opérations, l'ensemble M_{n, p}(K) a une structure d'espace vectoriel sur K de dimension np. L'élément neutre du groupe additif est la matrice nulle, généralement notée 0, qui vérifie ∀(i, j), α_ij = 0, et l'opposé de la matrice M = (α_ij) est la matrice, notée −M, égale à (−α_ij). Si M = (α_ij) est un élément de M_{n, p}(K) et N = (β_hi) un élément de M_{m, n}(K), alors le produit NM est défini par NM = (γ_hj), où . Pour obtenir l'élément de la h^ième ligne et de la j^ième colonne de NM, il faut donc faire la somme des produits d'un élément de la h^ième ligne de N par l'élément de la j^ième colonne de M de même indice, soit :

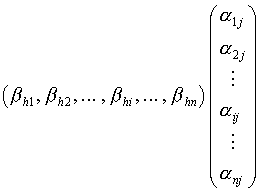
 ; on a alors :
γ_hj = β_h1 α_1j + β_h2 α_2j + … + β_hi α_ij + … + β_hn α_nj.
Cette multiplication entre matrices n'est évidemment pas commutative.

Structure de l'ensemble M_n(K)

Le produit de deux matrices carrées d'ordre n est toujours défini ; l'ensemble M_n(K) des matrices carrées d'ordre n, muni des opérations addition et multiplication des matrices, est donc un anneau unitaire. L'élément unité est la matrice unité, notée I_n, dont les éléments diagonaux sont égaux à 1, tous les autres éléments étant nuls. Cet anneau n'est pas commutatif et n'est pas intègre. Muni des trois opérations addition, multiplication et multiplication externe par un scalaire λ, il a une structure d'algèbre sur K. Ses éléments inversibles sont les matrices associées à des automorphismes ; on les appelle matrices carrées inversibles ou régulières.

Les matrices jouent un rôle important en algèbre linéaire (étude des applications linéaires, des endomorphismes, des automorphismes, des déterminants) et dans la résolution des systèmes d'équations linéaires. Elles trouvent également de nombreuses applications en physique et en analyse numérique (analyse théorique de la stabilité des méthodes de calcul numérique, résolution numérique des systèmes d'équations linéaires, des équations différentielles et aux dérivées partielles, etc.).