limite

Élément duquel se « rapprochent » les images d'une fonction (ou d'une suite), lorsque les antécédents correspondants se « rapprochent » d'une certaine valeur de l'ensemble de départ.

MATHÉMATIQUES

Limite d'une suite réelle

Si 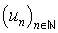est une suite réelle définie pour tout naturel au moins égal à un naturel donné n₀, on dit que ℓ est limite du (u_n) si,

.

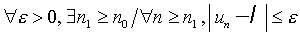
Limite d'une fonction numérique

Si f est une application de A ⊂ ℝ dans ℝ, et si a est adhérent de A, on dit que ℓ est la limite de f en a si,

.
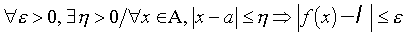
Cette notion de limite est indépendante de ce qui se passe au point a : f(a) peut aussi bien ne pas exister ou être différent de ℓ. La limite en a, si elle existe, se note
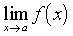ou .

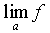Si f est définie et continue en a, ℓ est égal à f(a). Dans tous les cas, ℓ est adhérent à f(A).

Si on considère la restriction de f à la partie de A, intersection de A avec ] −∞, a [ (respectivement ] a, + ∞ [ ), la limite, lorsqu'elle existe, se nomme limite à gauche de f en a (respectivement limite à droite de f en a).

Limites à l'infini

Étant donné une application f de A (⊂ ℝ) dans ℝ, non majorée (respectivement non minorée), si 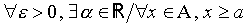(respectivement x ≤α)⇒ 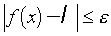, on dit alors que ℓ est la limite de f quand x tend vers + ∞ (respectivement − ∞) et on note
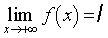(respectivement ).

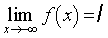Limites infinies

Si f est une application de A (⊂ ℝ) dans ℝ et si a est un élément de 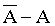ou un point de discontinuité, on peut avoir la propriété suivante : 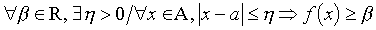(respectivement 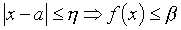). On dit alors que f a pour limite + ∞ (respectivement − ∞) en a.