géométrie
(latin geometria, du grec geômetria)

Pour Euclide, science des figures de l'espace ; pour F. Klein (programme d'Erlangen), étude des invariants d'un groupe de transformations de l'espace.
Origine et méthodes
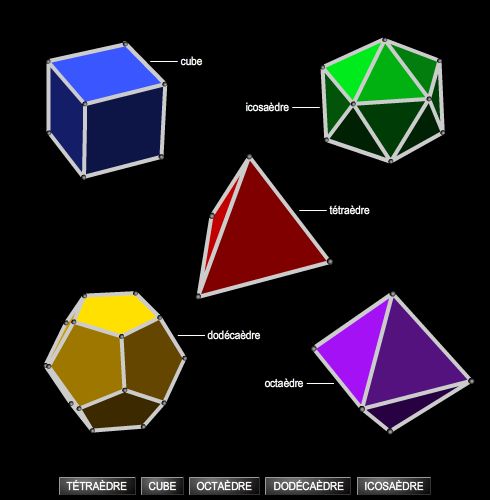
La géométrie, terme qui à l'origine signifie « mesure de la Terre », fut d'abord l'étude des figures dans le plan et dans l'espace. Bien que celles-ci dérivent d'objets concrets, la géométrie s'est très tôt refusé l'usage de méthodes expérimentales. Elle s'est au contraire évertuée à réduire les figures à une version idéale des objets réels : le point, la droite, etc. Elle a fait également appel à un mode de démonstration qui n'utilise ni l'observation ni la mesure mais qui fonctionne par postulats et conséquences. Depuis le xviie s., la géométrie a été façonnée par deux tendances contradictoires et complémentaires, l'une de diversification, l'autre d'unification. Elle s'est enrichie des apports conceptuels et des procédés développés dans les autres domaines des mathématiques, constituant de nouveaux champs d'investigation.
La géométrie euclidienne
Les origines de la géométrie se situent en Mésopotamie et en Égypte, mais c'est grâce aux Grecs qu'elle rompt (de 600 à 300 avant J.-C.) avec le pragmatisme des civilisations antérieures. La partie concernant la géométrie dans les Éléments d'Euclide en constitue l'exposé le plus complet et le plus achevé. Les postulats posés à la base de l'édifice assurent leur existence mais déterminent également les propriétés de l'espace euclidien. Dans l'école d'Alexandrie, rigueur euclidienne et techniques babyloniennes et égyptiennes s'allient dans une géométrie tournée davantage vers l'application.
Les Arabes s'approprient les connaissances grecques, les critiquent et les étendent sans cependant dépasser le cadre de la géométrie hellénistique. L'Europe médiévale, par leur intermédiaire, découvre les textes grecs. Au xve s., l'Occident accueille l'héritage grec conservé par les érudits byzantins. L'intégration de méthodes projectives est la première contribution des mathématiciens de la Renaissance au développement de la géométrie. Ce renouveau trouve son origine dans les pratiques des cartographes et des artistes. Peintres ou architectes mettent au point des règles telles que celles de la perspective, permettant de représenter dans un plan des figures de l'espace à partir du point que constitue l'œil.
Au xviie s. apparaissent les méthodes de géométrie analytique avec Descartes et Fermat. Dans sa Géométrie (1637), Descartes applique les méthodes algébriques à l'étude des courbes ; l'idée d'équation d'une courbe s'installe. Les techniques de calcul infinitésimal permettent d'examiner les propriétés qui varient d'un point à un autre.
Au xviiie s., la création par G. Monge de la géométrie descriptive, qui représente les points de l'espace par leurs projections orthogonales sur deux plans perpendiculaires entre eux, donne un nouvel élan à la géométrie projective. Dans cette voie, Poncelet et Chasles montrent l'importance du rôle des transformations, qui déforment les figures point par point, tout en conservant certaines propriétés.
Les géométries non euclidiennes
Jusqu'au xixe s., la géométrie euclidienne est censée rendre compte du monde sensible et ses résultats sont considérés comme absolument vrais. Au tournant du siècle, des savants comme J. H. Lambert, A. M. Legendre ou C. F. Gauss entrevoient la possibilité de construire, indépendamment des données de l'expérience, de nouvelles géométries logiquement cohérentes avec le système d'axiomes euclidien dans lequel on aurait remplacé le 5e postulat des parallèles par sa négation. N. I. Lobatchevski (1826) et J. Bolyai (1832-1833) font les premiers exposés systématiques de cette « géométrie non euclidienne », qui repose sur l'hypothèse d'une infinité de parallèles par un point extérieur à une droite donnée (géométrie hyperbolique). La géométrie elliptique, déduite de l'hypothèse qu'il n'y a aucune parallèle, est étudiée par B. Riemann. La conception riemannienne de l'espace préfigure celle de la relativité générale.
La géométrie axiomatique

F. Klein, en 1872, se propose d'établir un principe général (la recherche des propriétés invariantes) d'après lequel on puisse édifier les deux géométries : métrique et projective. Il caractérise chacune par un groupe de transformations, l'identifie à l'étude des invariants de ce groupe et aboutit à la hiérarchie suivante : 1° la géométrie projective ; 2° la géométrie affine ; 3° la géométrie métrique ; 4° la géométrie euclidienne ; 5° situées au même niveau que la géométrie affine : a) les géométries non-euclidiennes, appelées par Klein « géométrie métrique hyperbolique » ; b) la géométrie métrique parabolique.
Partant d'axiomes différents, ces dernières géométries sont irréfutables sur le plan logique mais deux à deux contradictoires. C'en est fini de plus de deux millénaires d'« évidences » mathématiques. D. Hilbert, avec ses Fondements de la géométrie (1900), instaure les bases de la méthode axiomatique et règle la question des contradictions : les axiomes d'une théorie mathématique ne sont plus des vérités évidentes ou non, mais des relations, auxquelles on attribue la valeur « vrai », en se souciant uniquement de la compatibilité des axiomes les uns avec les autres.
Au xxe s., la géométrie liée à l'algèbre par l'intermédiaire des coordonnées, de la théorie des ensembles et l'étude des structures (de groupe, de corps, etc.) prend figure de géométrie algébrique, enrichie d'emprunts à l'analyse et à la topologie. Celle-ci, dans la conception de Klein, est la géométrie des invariants du groupe des transformations ponctuelles continues. Les recherches de É. Cartan et de S. Lie introduisent la géométrie différentielle et infinitésimale. A. Connes fonde la géométrie non commutative, qui fournit un cadre approprié à la résolution de certains problèmes posés par la physique quantique.