mécanique ondulatoire ou mécanique quantique (suite)

Fonction d’onde et probabilité

Le but de la mécanique classique est de décrire les mouvements des corpuscules matériels en calculant à chaque instant t leurs positions repérées par leurs trois coordonnées dans l’espace x, y, z. La mécanique ondulatoire renonce à calculer directement les coordonnées ; mais elle associe à chaque corpuscule matériel une fonction des coordonnées et du temps ψ (x, y, z, t), appelée fonction d’onde et dont on peut déduire une information sur la localisation du corpuscule au moyen de la règle suivante : la probabilité de trouver le corpuscule dans un cube de volume dV centré sur le point x, y, z est égale à
|ψ (x,y,z,t)|² dV = ψ (x,y,z,t) · ψ* (x,y,z,t) · dV
(on sait qu’on obtient le carré du module d’une fonction complexe ψ en la multipliant par la fonction imaginaire conjuguée ψ*). Par définition, la probabilité de trouver la particule dans l’espace entier est égale à 1, c’est-à-dire que la fonction ψ doit être normée de telle sorte que l’on obtienne l’unité en intégrant l’expression ci-dessus dans l’espace entier :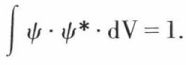

Dans le cas d’un système physique compliqué comportant plusieurs particules que nous pouvons numéroter 1, 2, 3, etc., et qui interagissent fortement entre elles, il n’est généralement pas possible de définir une fonction d’onde séparée pour chaque particule. Mais on utilise une fonction d’onde globale du système, dépendant des coordonnées de toutes les particules :
ψ (x₁, y₁, z₁, x₂, y₂, z₂, x₃, y₃, z₃, ..., t)
et on calcule la probabilité de trouver simultanément la particule 1 dans un cube de volume dV₁ autour du point x₁, y₁, z₁, la particule 2 dans un cube de volume dV₂ autour du point x₂, y₂, z₂, etc., par l’expression :
ψ · ψ* · dV₁ · dV₂ · dV₃ ...,
c’est-à-dire que la probabilité de trouver la particule 1 au point x₁ y₁ z₁ dépend des positions des autres particules 2, 3, etc., et réciproquement.

Grandeur observable et opérateur

Lorsqu’on effectue des expériences, on n’observe pas seulement des positions de particules. Le plus souvent même on mesure d’autres grandeurs, individuelles ou collectives : impulsion, moment cinétique, énergie, etc. Très souvent, ces grandeurs varient avec les coordonnées des particules : et comme ces dernières ne sont pas calculables de manière exacte, on ne peut définir qu’une valeur moyenne de la grandeur G, moyenne effectuée sur les diverses positions possibles de la particule en tenant compte de leurs probabilités.

Pour effectuer une mesure de la grandeur G, il faut effectuer une certaine opération sur le système physique étudié. Cette opération peut être représentée dans la théorie par un opérateur mathématique, souvent désigné par la même lettre G. Cet opérateur symbolise une certaine manière de transformer les fonctions de l’espace et du temps ψ (x, y, z, t) en d’autres fonctions ; c’est-à-dire qu’on se donne une règle permettant de remplacer chaque fonction ψ (x, y, z, t) par une autre que l’on calcule à partir d’elle. Un exemple fera mieux comprendre ce dont il s’agit : l’impulsion d’une particule est un vecteur 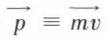qui se projette sur les axes selon trois composantes p_x, p_y, p_z, qui sont trois grandeurs mesurables dans des expériences. À la grandeur observable p_x on associe l’opérateur mathématique (i désigne la base des nombres complexes, ħ est la constante de Planck h divisée par 2 π) ; appliquer cet opérateur à la fonction ψ, c’est la remplacer par la fonction obtenue en multipliant par – iħ sa dérivée partielle par rapport à x ;

Connaissant l’opérateur G associé à la grandeur observable G, nous pouvons appliquer la règle qui permet le calcul de la valeur moyenne < G > : on fait le produit de la fonction d’onde imaginaire conjuguée ψ* par la fonction Gψ obtenue en appliquant l’opérateur G ; puis on calcule l’intégrale de ce produit sur l’espace entier :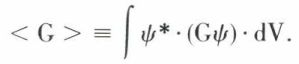

Nous n’essaierons pas d’expliquer comment a pu être établie la correspondance entre les diverses grandeurs observables et les opérateurs qui les représentent.

Nous ne pouvons pas non plus détailler les propriétés mathématiques de ces opérateurs. Nous ferons à ce sujet deux remarques seulement :

1. Lorsqu’on est amené à former un opérateur en combinant plusieurs autres opérateurs, il faut prendre garde à l’ordre suivant lequel on les utilise.

L’opérateur 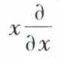par exemple, appliqué à la fonction ψ, représente deux opérations successives : la multiplication par x de sa dérivée. Tandis que l’opérateur conduit à un résultat différent ; appliqué à ψ, il représente la dérivée de la fonction xψ :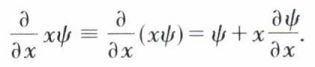

Ainsi, l’ordre dans lequel on applique les deux opérateurs x et 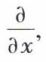pour former les opérateurs plus complexes 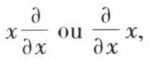n’est pas indifférent ; on dit que les deux opérateurs x et ne commutent pas entre eux. L’ordre dans lequel on applique les deux opérateurs y et 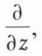au contraire, est indifférent ; on dit que les opérateurs y et commutent entre eux. Les règles de commutation des opérateurs ont une grande importance en mécanique quantique.

2. Bien que la transformation subie par la fonction ψ sous l’action de l’opérateur G résulte d’une opération souvent complexe, cela n’empêche pas que le résultat de cette transformation puisse être très simple, si la fonction ψ possède certaines formes particulières. Ainsi on peut trouver telle fonction ψ (x, y, z, t) qui par application de l’opérateur G se transforme en elle-même, multipliée par un coefficient numérique k :
G ψ = ψ · k.
On dit que cette fonction ψ est une fonction propre de l’opérateur G, et que le coefficient numérique k est la valeur propre correspondante. Si le système physique étudié se trouve dans un état qui est représenté par cette fonction ψ, on dit qu’il est dans un état propre de l’opérateur G ; et dans le langage courant on confond fréquemment les termes de fonction propre et d’état propre. En appliquant la définition donnée plus haut pour la valeur moyenne < G > de la grandeur observable, il est facile de voir que la valeur moyenne < G > mesurée dans l’état propre ψ est égale à la valeur propre correspondante k. Il est également facile de montrer que tous les opérateurs qui commutent entre eux possèdent les mêmes fonctions propres.