Maxwell (équations de) (suite)
Si maintenant on considère les champs  et
et  en un point M, fixe pour R, les champs
en un point M, fixe pour R, les champs 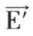 et
et  mesurés en M par un observateur de R′ sont donnés par les relations suivantes :
mesurés en M par un observateur de R′ sont donnés par les relations suivantes :
dans lesquelles  sont les composantes de
sont les composantes de  parallèles à
parallèles à  et
et  les composantes normales à
les composantes normales à  Ces transformations sont beaucoup plus compliquées qu’avec les quadrivecteurs, d’où l’idée de chercher à n’utiliser que ces derniers. Les potentiels
Ces transformations sont beaucoup plus compliquées qu’avec les quadrivecteurs, d’où l’idée de chercher à n’utiliser que ces derniers. Les potentiels  et V en donnent la possibilité.
et V en donnent la possibilité.
L’équation (16) s’écrit compte tenu de (15) et (18)
Or, si on pose u = jct, il vient
d’où 
A apparaît comme un quadrivecteur, et on écrira
□ A se lisant : « d’alembertien de  ».
».
De même, l’équation (17) devient :
Vu (18),  soit
soit 
On peut fondre en une seule équation (16′) et (17′). Soit en effet une charge volumique ρ0 fixe pour R′. Pour R, elle apparaît comme valant
et crée au point M(x, y, z, t) la densité de courant  dont les composantes dans R sont
dont les composantes dans R sont
On peut introduire la 4e coordonnée de M ; u = jct, d’où la 4e composante de 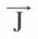 :
:
Or, de (17′), il vient :
Par ailleurs, de (16′), il vient :
Finalement, si nous formons :
— d’une part le quadrivecteur potentiel 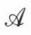 dont les composantes sont Ax, Ay, Az et
dont les composantes sont Ax, Ay, Az et  c’est-à-dire dont les composantes spatiales sont celles de
c’est-à-dire dont les composantes spatiales sont celles de  et la composante imaginaire
et la composante imaginaire 
— d’autre part le quadrivecteur source  dont les composantes sont Jx, Jy, Jz et jcp (c’est-à-dire J et jcp), les équations 17″ et 16″ se fondent en
dont les composantes sont Jx, Jy, Jz et jcp (c’est-à-dire J et jcp), les équations 17″ et 16″ se fondent en
forme la plus condensée des équations de Maxwell. Elle implique (15) et (18).
Sous cette forme de quadrivecteurs, le passage d’un référentiel R à un R′ se fera plus facilement (G2). On reviendra à  et
et  par
par  et
et
Potentiels retardés
Considérons une région de l’espace dépourvue de charges  (16) et (17) deviennent
(16) et (17) deviennent
Ce sont des équations de propagation. Les potentiels se propagent à vitesse
Envisageons par exemple une charge ponctuelle q placée en un point O et capable de varier (fig. 7). Le potentiel qu’elle crée en M variera, mais avec un décalage dans le temps  par rapport aux variations de q. Plus précisément, le potentiel à l’instant t en M sera
par rapport aux variations de q. Plus précisément, le potentiel à l’instant t en M sera
où  représente la charge en O à l’instant
représente la charge en O à l’instant 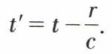

Plus généralement, on vérifiera que toute fonction  satisfait bien a
satisfait bien a 
 représente une propagation dans le sens des r positifs (O vers M sur la figure) ;
représente une propagation dans le sens des r positifs (O vers M sur la figure) ;  une propagation dans le sens des r négatifs, qui n’a pas de signification dans l’exemple actuel.
une propagation dans le sens des r négatifs, qui n’a pas de signification dans l’exemple actuel.
La fonction VM est dite « fonction potentiel retardé ». Il en va de même du potentiel vecteur  Si, dans le volume dv entourant O, il existe une densité de courant
Si, dans le volume dv entourant O, il existe une densité de courant  fonction du temps t, le potentiel
fonction du temps t, le potentiel  résultant en M sera
résultant en M sera
Ondes électromagnétiques dans un milieu diélectrique infini non chargé
• Milieu parfait : μ et ε sont des constantes, et γ ≡ 0. et V se propageant, il en est de même de
et V se propageant, il en est de même de  et
et  D’ailleurs, les équations (1) (2) (3) (4) devenant
D’ailleurs, les équations (1) (2) (3) (4) devenant
on en tire
On retrouve bien les équations de propagation à vitesse 
En cas particulier, on peut examiner une propagation en ondes planes, c’est-à-dire se faisant selon une seule direction (Oz par exemple sur la figure 8). En tout point d’un plan parallèle à Ox, Oy, on retrouve les mêmes états de vibration pour  (et pour
(et pour  ). Autrement dit,
). Autrement dit, 

Or, 
Par suite Ez = 0. Le champ  est normal à Oz. Choisissons alors l’axe Ox parallèle à
est normal à Oz. Choisissons alors l’axe Ox parallèle à 
De  il vient
il vient
À une constante près (qui correspondrait à une absence de propagation).
Hx = 0, Hz = 0.
Le champ H est parallèle à l’axe Oy.
Finalement, les deux champs 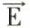 et
et  se propagent perpendiculairement l’un à l’autre et sont de plus perpendiculaires à la direction de propagation Oz. Plus précisément, le trièdre
se propagent perpendiculairement l’un à l’autre et sont de plus perpendiculaires à la direction de propagation Oz. Plus précisément, le trièdre  est direct. En outre, le rapport
est direct. En outre, le rapport  est indépendant du temps en tout point et vaut
est indépendant du temps en tout point et vaut  impédance du milieu. Si E et H sont des fonctions sinusoïdales du temps, elles sont en phase.
impédance du milieu. Si E et H sont des fonctions sinusoïdales du temps, elles sont en phase.
Enfin, l’énergie volumique électromagnétique vaut
Elle se propage dans le sens de  , c’est-à-dire du vecteur
, c’est-à-dire du vecteur  et a pour valeur instantanée
et a pour valeur instantanée 
P est dit « vecteur de Poynting ».
• Milieu imparfait : ε n’est plus une constante, et l’équation (2) devient :
Dans le cas général, on ne sait pas résoudre les équations. Cependant, lorsque E est une fonction sinusoïdale du temps de la forme E = Em · cosωt, on peut écrire avec une approximation D = Dm cos (ωt + θ), ce qui revient à assimiler à une ellipse la courbe D = f(E), cycle d’hystérésis diélectrique. On peut alors utiliser les notations imaginaires D = ε · E, où ε est maintenant une constante, mais complexe. On est ramené à l’étude précédente avec une vitesse complexe
et une équation de propagation
La solution, pour une onde plane, est de la forme E = E0 e– ax e j (ωt + bx), avec  cos φ et
cos φ et 
Parallèlement, H = H0 e– ax e j(ωt + bx).
Les ondes sont progressivement absorbées par le milieu, leur énergie se transformant en chaleur par pertes diélectriques.
C. T.




