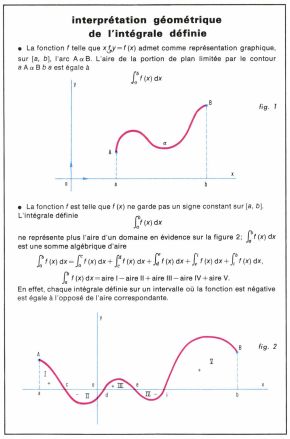
intégrale définie (suite)

4. Si f et g sont intégrables sur (a, b), f + g l’est aussi et

Par application de la propriété 3 et de la propriété 4, itérée, on trouve :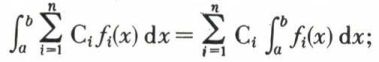

ce qui permet, par exemple, de calculer l’intégrale définie d’un polynôme sur un intervalle donné, comme somme des intégrales des différents monômes de ce polynôme.

5. Formules de la moyenne.
Première formule. Si f et g sont intégrables sur (a, b) et f (x) garde un signe constant sur (a, b),

m et M étant respectivement les bornes inférieure et supérieure de g dans (a, b).
Si g est continue, il existe une quantité ℰ, 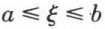telle que K = g(ξ) ; par suite,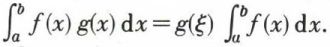

Un cas très fréquent est celui où f = 1 ; on a alors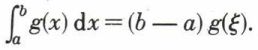

Deuxième formule. Si f est une fonction non croissante sur (a, b) et f (x) > 0 ; si g est intégrable, on a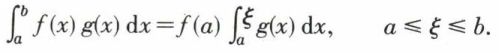

6. Intégrale définie fonction de ses bornes.
De sa borne supérieure. La fonction F telle que

est continue en un point x₀ quelconque d’un intervalle (a, b) où f est intégrable, car, d’après la première formule de la moyenne, on a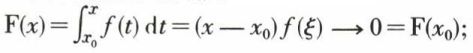

quand x → x₀, f étant bornée, d’où la continuité.
De plus,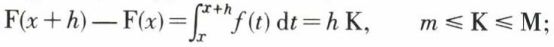
quand h → 0, f (x + h) → f (x + 0), ou f (x + h) → f (x – 0),
suivant que h → 0⁺ ou h → 0^–, f (x + 0) et f (x – 0) désignant les limites correspondantes de f (x) ; dans les mêmes conditions, K → (x ± 0), et, par suite,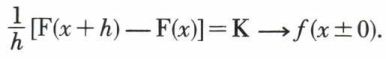

La fonction F admet donc une dérivée à droite et une dérivée à gauche, au point x, respectivement égales à f (x + 0) et f (x – 0). Si f est continue sur l’intervalle d’intégration, ce qui est souvent le cas, K = f (x), et, si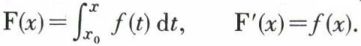

La fonction F est alors une primitive de la fonction f. Le calcul des intégrales définies est donc ramené, dans la plupart des cas, à celui des primitives.
De sa borne inférieure. Si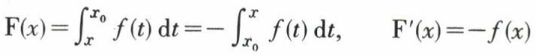

d’après le résultat précédent.
De ses deux bornes. Si a(x) et b(x) sont deux fonctions de x dérivables, et si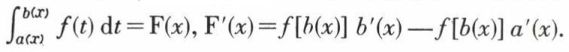

7. Si G est une primitive de f sur (a, b), 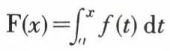en est une autre ; par suite, F(x) = G(x) + C, puisque F et G ont la même dérivée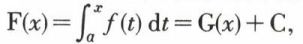

mais, pour x = a, F(a) = 0, d’où 0 = G(a) + C, d’où C = – G(a) et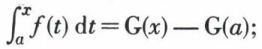

par suite,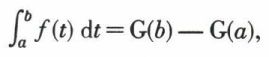

noté aussi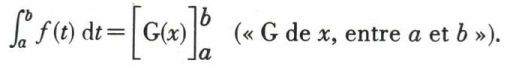

Il suffit, pour calculer une intégrale définie, de connaître une primitive de la fonction sous le signe somme ∫, ce qui n’est pas toujours possible.

Calcul des primitives

Comme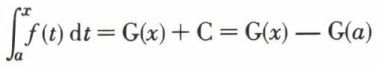

et que toutes les primitives de f sont de la forme G(x) + C, on désigne une primitive quelconque de f par ∫ f (x) dx, sans préciser la borne inférieure a, puisqu’on sait qu’il suffit de prendre C = – G(a), ni la borne supérieure x, puisqu’elle est quelconque, et l’on écrit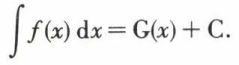

Intégration par parties

Si u′(x) et v′(x) sont les dérivées, bornées et continues, de u(x) et v(x), la relation (uv)′ = u′v + v′u donne, par intégration entre a et b :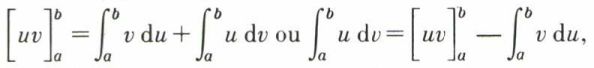

qui est la formule d’intégration par parties ; elle est valable pour une intégrale indéfinie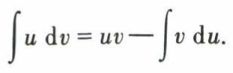

Exemples.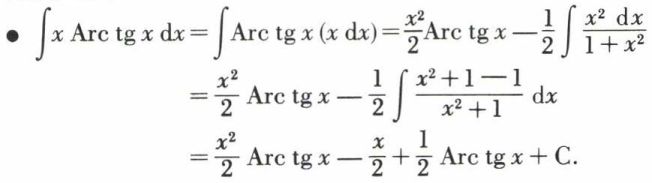

Une telle méthode est souvent fructueuse quand la fonction sous le signe somme comporte une fonction transcendante dont la dérivée est au moins algébrique, Log x, Arc sin x ... D’autre part, s’il s’agit d’une intégrale définie, il peut se faire que le terme tout intégré soit nul, ce qui donne une relation entre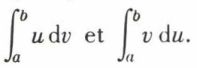

Ce cas se présente souvent quand on cherche une relation de récurrence permettant le calcul d’une intégrale I_n dépendant d’un entier n.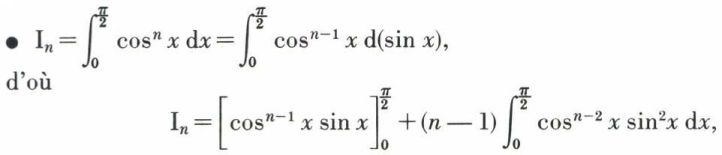

et I_n = (n – 1) (I_n–2 – I_n), car la quantité entre crochets est nulle et sin² x = 1 – cos² x, d’où la relation nI_n = (n – 1)I_n–2, qui permet le calcul de I_n.

Changement de variable

Si x = φ(t) est une fonction continue monotone, à dérivée continue, sur l’intervalle [t₀, t₁], avec φ(t₀) = a, φ(t₁) = b, et si f (x) est continue sur [a, b],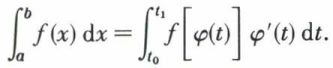

En effet, f (x) dx est une véritable différentielle et, par le changement de variable x = φ(t), la différentielle est invariante
f (x) dx = f [φ(t)] φ′(t) dt.
Cette méthode est très employée.

Exemples.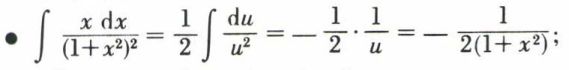

en effet, si u = x² + 1, du = 2x dx.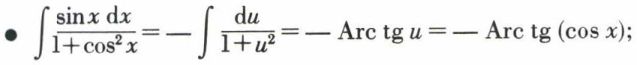

en effet, si u = cos x, du = – sin x dx.
De tels changements de variables sont à essayer quand on a à calculer une intégrale de la forme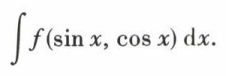

Règles. Si, f étant rationnelle, f (sin x, cos x) dx ne change pas quand on remplace :
x par π – x, on pose sin x = u, ou x = Arc sin u ;
x par – x, on pose cos x = u, ou x = Arc cos u ;
x par π + x, on pose tg x = u, ou x = Arc tg u ;
si aucun des changements n’est concluant, on pose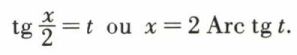

Cependant, il faut faire attention aux discontinuités qu’introduit ce changement de variable.

Intégrales généralisées

• L’intervalle d’intégration est infini.
Pour α ≠ 1,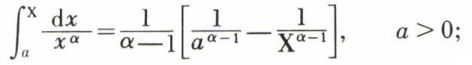
quand x → ∞, le second membre a un sens si α > 1, car 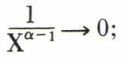on dit que l’intégrale 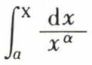converge, et l’on note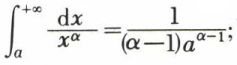
pour α = 1,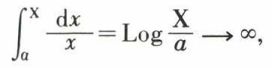
quand x → + ∞.

Par suite, si pour x > X, | f (x) | x^α < C, C constant, α > 1, existe.

Une condition nécessaire de convergence de 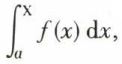quand X → ∞, est donc que | f (x) | → 0 ; elle n’est pas suffisante.

• La fonction à intégrer ne reste pas bornée au voisinage d’une borne d’intégration.
Pour α ≠ 1,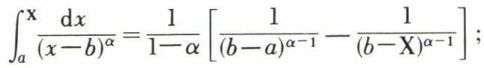
quand X → b^–, le second membre a un sens si α < 1, et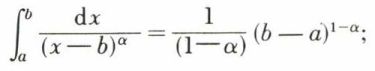

pour α = 1,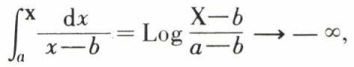
quand X → b^–.

Par suite, si quand x → b, | f (x) | (b – )^α < K, avec α < 1, 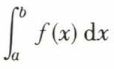existe.

E. S.

➙ Calcul numérique / Différentielle / Fonction / Série.