Hermite (Charles) (suite)
Hermite, qui introduisait des variables continues en théorie des nombres, découvre en 1853, pour les besoins de cette théorie, les formes hermitiennes, qui se sont révélées après 1925 indispensables au développement de la mécanique quantique, et inaugure par ailleurs avec les Anglais Arthur Cayley (1821-1895) et James Joseph Sylvester (1814-1897) la théorie algébrique des invariants.
De 1848 à 1850, il enseigne au Collège de France, à titre provisoire. C’est au cours de cet enseignement qu’il définit in abstracto les fonctions elliptiques comme fonctions méromorphes à double période, en Utilisant pour leur étude l’intégrale de Cauchy. De 1862 à 1867 maître de conférences à l’École normale supérieure, il succède, en 1869, à Jean-Marie Constant Duhamel (1797-1872) comme professeur d’analyse à l’École polytechnique et d’algèbre supérieure à la Sorbonne. Dans cette dernière chaire, son enseignement a, pendant près de trente ans, un retentissement considérable tant en France qu’à l’étranger.
Ses travaux portent sur les parties les plus abstraites des mathématiques : théorie des nombres, en particulier étude des formes quadratiques, fonctions elliptiques, dont il montre les liens étroits avec l’arithmétique supérieure, fonctions modulaires, abéliennes, algébriques. Les fonctions modulaires sont le premier exemple des fonctions automorphes où devait s’illustrer Henri Poincaré*.
Celle de ses études qui frappa le plus le grand public mathématique est, en 1873, sa démonstration de la transcendance du nombre e, base des logarithmes népériens.
Membre de l’Académie des sciences (1856), il n’abandonne sa chaire de la Sorbonne qu’en 1897, et y est remplacé par son gendre, Émile Picard (1856-1941).
J. I.





 et
et  d’un espace vectoriel En de dimension n sur le corps ℂ des complexes est le scalaire de ℂ, noté
d’un espace vectoriel En de dimension n sur le corps ℂ des complexes est le scalaire de ℂ, noté  tel que :
tel que : la barre indiquant le conjugué ;
la barre indiquant le conjugué ;
 et
et 
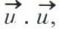 noté
noté  est un nombre positif pour tout
est un nombre positif pour tout 
 si et seulement si
si et seulement si 



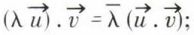
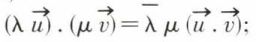

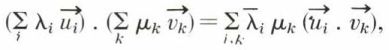
 et
et  pour i = 1,2 ..., p ; et k = 1,2,..., q.
pour i = 1,2 ..., p ; et k = 1,2,..., q. et
et  étant rapportés à la base
étant rapportés à la base  rapportés à la base
rapportés à la base 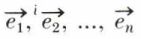 de l’espace En, en appliquant la distributivité généralisée, on obtient :
de l’espace En, en appliquant la distributivité généralisée, on obtient :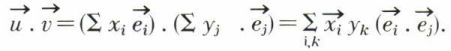
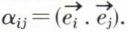 Mais il ne faut pas en conclure que
Mais il ne faut pas en conclure que 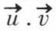 dépend de la base choisie ;
dépend de la base choisie ;  le nombre positif
le nombre positif 

 il existe un vecteur
il existe un vecteur  normé, colinéaire à
normé, colinéaire à 
 est orthonormée et seulement dans ce cas,
est orthonormée et seulement dans ce cas,  pour
pour 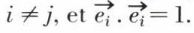 Il en résulte que
Il en résulte que
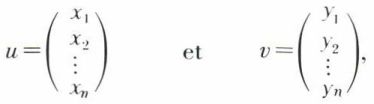
 les transformés de
les transformés de 





 Une matrice unitaire conserve la norme puisqu’elle conserve le produit scalaire, donc, en particulier, la carré scalaire,
Une matrice unitaire conserve la norme puisqu’elle conserve le produit scalaire, donc, en particulier, la carré scalaire, 
 (les deux opérations commutent).
(les deux opérations commutent).