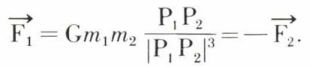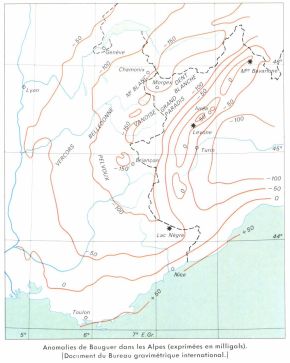
Historiquement, dès les premières expériences, au xviii^e s., on a remarqué l’influence considérable du relief avoisinant les stations sur les anomalies à l’air libre. Une correction simple, dite « correction de Bouguer », consiste à ramener les mesures au niveau zéro et à éliminer, en chaque station, le relief environnant : on aboutit ainsi aux anomalies de Bouguer, assez régulières, dont on dresse systématiquement des cartes détaillées. Une analyse plus poussée indique que, en général, les anomalies de Bouguer sont positives sur les océans et négatives sur les hauts reliefs. Cela semble prouver que, sous les océans, il y a surcroît de masses et, au-dessous des reliefs, déficit de masses. Une explication possible de ce résultat est donnée par la théorie de l’isostasie. La théorie isostatique n’est en fait qu’une hypothèse de travail, en général assez bien vérifiée. Si on l’adopte, on est amené à corriger les anomalies de Bouguer de l’influence du relief interne supposé. La valeur corrigée Δg prend le nom d’anomalie isostatique. En assimilant le géoïde à une sphère, on établit la relation suivante :

La fonction de l’arc sphérique MP reliant le point courant P au point M où l’on désire calculer le potentiel T a une expression donnée en 1849 par sir George Gabriel Stokes. Cette formule donne la valeur du champ perturbateur T, donc celle de la cote N, par rapport à l’ellipsoïde de référence, supposé centré au centre de gravité des masses terrestres. Des formules du même type, valables au niveau de la surface topographique, sont applicables aux anomalies à l’air libre (M. S. Molodenski, 1947). La principale difficulté d’application réside dans le fait que les mesures de gravité n’existent pas en de nombreux points du globe, ou ne sont pas publiées.

Utilisation locale des anomalies

On peut d’abord utiliser les mesures détaillées de l’intensité g de la pesanteur dans une région donnée pour avoir les ondulations locales du géoïde, en particulier ses variations de pente (déviations de la verticale) rapportées au centre de gravité des masses. On peut ainsi corriger localement les verticales astronomiques, ce qui permet de s’en servir pour définir la cartographie (procédé employé en particulier en U. R. S. S.).

Les anomalies locales servent aussi à détecter des différences de densité dans le sous-sol. La théorie mathématique indique que la donnée des valeurs de g à la surface topographique ne permet absolument pas de connaître le détail des densités en profondeur, mais, grâce à des hypothèses supplémentaires, on peut mettre en évidence, avec une certaine probabilité, des formations particulières telles que des nappes pétrolifères ou des coulées volcaniques de forte densité.

Les résultats gravimétriques permettent de détecter des régions où la théorie isostatique ne s’applique pas, et sont à la base d’expériences complémentaires pour préciser les hypothèses formulées.

H.-M. D.

➙ Ellipsoïde de référence / Géodésie / Géoïde / Isostasie.

 P. Lejay, Développements modernes de la gravimétrie (Gauthier-Villars, 1947). / J. Goguel, la Gravimétrie (P. U. F., coll. « Que sais-je ? », 1963 ; 2^e éd., 1972). / M. Caputo, The Gravity Field of the Earth from Classical and Modern Methods (Londres, 1967). / W. Heiskanen et H. Moritz, Physical Geodesy (San Francisco et Londres, 1967). / J. J. Levallois, Géodésie générale (Eyrolles, 1969 ; 4 vol.).

Deux grands noms de la gravimétrie

mathématicien et physicien irlandais (Bornat Skreen 1819 - Cambridge 1903). Professeur de mathématiques à l’université de Cambridge (1849), membre de la Société royale de Londres en 1851, il est l’auteur de travaux sur l’hydrodynamique, l’optique et les rayons X. Son nom est resté attaché à deux formules. La première permet, en mathématiques, de ramener une intégrale de surface, limitée par un contour, à une intégrale curviligne sur ce contour. La deuxième, établie en 1849, permet, en gravimétrie, de calculer la différence de cote entre géoïde et ellipsoïde par une intégrale appliquée aux anomalies de la pesanteur et étendue à la totalité du globe.

géophysicien et géodésien néerlandais (La Haye 1887 - Amersfoort 1966). Professeur de géodésie à l’université d’Utrecht (1927), puis à Delft (1939), membre de l’Académie royale des sciences et président de l’Association internationale de géodésie (1933-1946), il imagine en 1920 une méthode de mesure de la pesanteur en mer à l’aide de deux pendules oscillant en opposition de phase. On lui doit plusieurs théories sur l’origine des chaînes de montagnes (plis-racines) ainsi que des formules donnant les déviations de la verticale à partir de la formule de Stokes.