différentielle (suite)

Notation

La différentielle de y = f(x) est notée dy (on lit « dy ») ; la dérivée en un point x quelconque est notée y′_x ou f ′(x) ; h désignant un facteur arbitraire, dy = f ′(x)h. Si y = x, f ′(x) = 1 ; dy = dx = h. On adopte alors, dans tous les cas, la notation dy = f ′(x)dx.

Propriétés de la différentielle

1^o Si f ′(x) est non nulle et si dx désigne un infiniment petit, dy est équivalent à l’accroissement Δy de la fonction f correspondant à l’accroissement dx de la variable x. En effet, quand dx tend vers zéro, f ′(x) est la limite de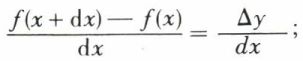

par suite,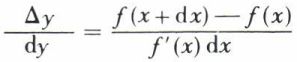

tend vers 1 quand dx tend vers zéro, ce qu’on écrit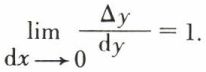

L’accroissement Δy est donc équivalent à la différentielle dy.

2^o La différentielle dy est égale à f ′(x)dx, que x soit ou ne soit pas la variable indépendante. En effet, si dans y = f(x) on effectue le changement de variable x = φ(t), φ(t) étant dérivable, on peut calculer dx = φ′(t) dt, et par suite, comme dy = f ′(x) dx, on a dy = f_x . x_t dt ; mais f ′_x . x′_t est la dérivée de la fonction composée y = f[φ(t)] par rapport à t, de sorte que dy = y′_t dt, que l’on peut considérer comme ayant été obtenu en appliquant directement la définition de la différentielle à la fonction y(t). C’est cette propriété d’invariance de la différentielle qui en fait l’intérêt.

3^o Les théorèmes donnant les règles de dérivation des fonctions d’une variable donnent des règles de différentiation :

• d(x^m) = m x^m–1 dx ;

• si u et v sont deux fonctions de x,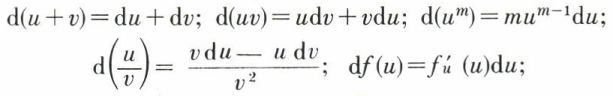

exemple : y = Arc tg u,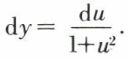

4^o Dans le cas de différentielles d’ordre supérieur à 1, la différentielle dy = f ′(x) dx est la différentielle première, appelée simplement différentielle. On peut définir, dans le cas où la fonction f est n fois dérivable, la différentielle seconde, puis, par récurrence, la différentielle d’ordre n. Ainsi, d(dy), qui est la différentielle seconde, est définie par
d (dy) = d (y′_xdx) = dy′_x dx + y′_xd (dx) ;
on note :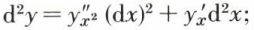
si x est la variable indépendante, on considère dx comme étant constant, d’où d (dx) = 0 et 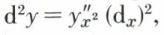, noté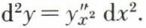
On définit alors dⁿ(y) = d (d^n–1y), différentielle d’ordre n.

Les différentielles d’ordre quelconque fournissent, quand x est la variable indépendante, une notation pour les dérivées successives d’une fonction notée y. En effet, de dy = f ′(x)dx = y_x dx, on tire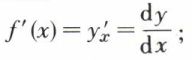

de même, 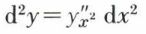fournit 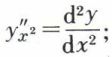de façon générale, la dérivée d’ordre n, y⁽ⁿ⁾ (x), est notée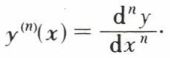

Applications de la différentielle

• On peut confondre, au premier ordre, l’accroissement Δy d’une fonction avec sa différentielle dy, ce qui est souvent utilisé en physique.

• La principale application de la différentielle se trouve dans les changements de variables (propriété d’invariance), que l’on utilise surtout pour le calcul des intégrales et aussi dans la résolution des équations différentielles. Ainsi l’équation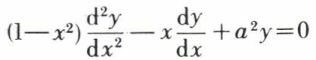

devient, par le changement de variable x = sin t pour l’équation à coefficients constants 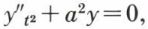dont la solution est y = A sin (at + B). En effet,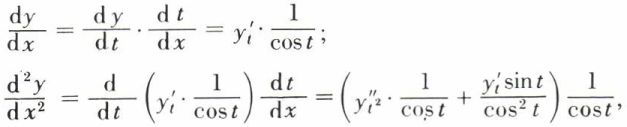
qu’il suffit de porter dans l’équation initiale.

Différentielle d’une fonction de plusieurs variables

La différentielle d’une fonction f(x, y, z), par exemple, est la quantité, notée df, définie par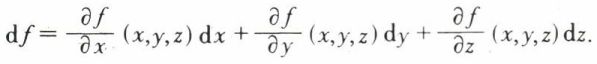

Cette définition suppose l’existence des trois dérivées partielles

Dans une dérivée partielle, on suppose que toutes les variables ont une valeur fixée, sauf une, et on dérive par rapport à cette dernière. Ainsi, la dérivée partielle par rapport à z de la fonction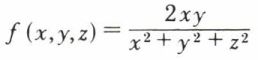

a pour expression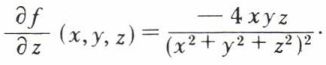

Si une fonction est différentiable, elle est continue et admet des dérivées partielles premières par rapport à toutes les variables ; inversement, si une fonction admet des dérivées partielles premières continues, elle est différentiable.

Tout ce qui vient d’être dit s’applique aux fonctions de n variables ; les cas les plus courants sont n = 2 et n = 3.

Exemple :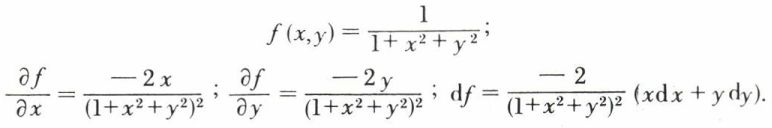

Propriétés de la différentielle

• Invariance. Si dans f (x, y, z) on fait le changement de variables x = x (u, v), y = y (u, v), z = z (u, v), la fonction
F(u, v) = f [x (u, v), y (u, v), z (u, v)]

a encore comme différentielle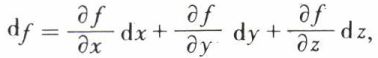

à condition que dx, dy et dz soient remplacés par les différentielles de x, y et z et que toutes les dérivées partielles utilisées soient continues. En effet,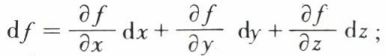

Cette invariance fait l’intérêt de la différentielle.

• Différentielles d’ordre supérieur à 1. Pour une fonction de deux variables, par exemple 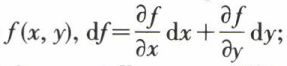on peut définir, sous réserve de la continuité des dérivées partielles, une différentielle seconde, puis une différentielle d’ordre n. Ainsi,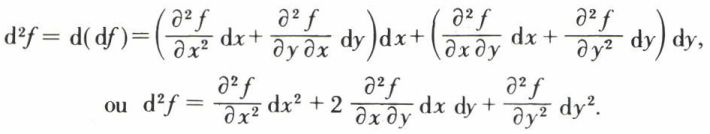

Les notations 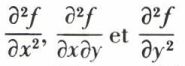désignent les dérivées partielles secondes de f (x, y) ; de plus, 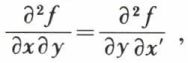car ces dérivées sont continues. Le calcul précédent suppose que x et y sont les variables indépendantes et que, par suite,
d²x = d²y = 0.
Si l’on effectuait le changement de variables x = x (u, v) et y = y (u, v), f (x, y) deviendrait F(u, v), dont la différentielle seconde serait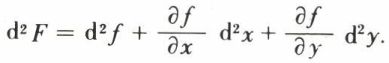

De façon générale, x et y étant les variables indépendantes, la différentielle d’ordre n, dⁿf, de la fonction f (x, y) est égale à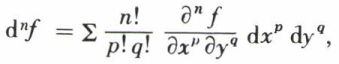

la somme étant étendue à toutes les valeurs de p et q telles que p + q = n, p et q étant entiers. On écrit aussi

l’exposant (n) étant une puissance symbolique imposant le développement de l’expression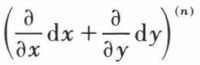

suivant la formule du binôme de Newton, mais en remplaçant tous les produits de la forme

Par exemple,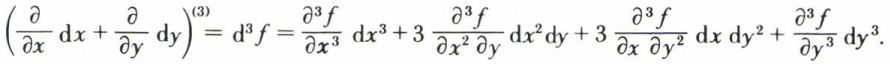

• Condition pour qu’une forme différentielle soit une différentielle totale exacte. La forme W = P(x, y) dx + Q(x, y) dx est la différentielle d’une fonction f (x, y) si, et seulement si, 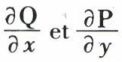étant continues, on a l’identité 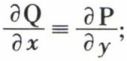la forme W = P(x, y, z) dx + Q(x, y, z) dy + R(x, y, z) dz est la différentielle d’une fonction f (x, y, z) si, et seulement si, on a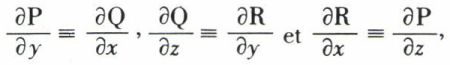

sous réserve de la continuité des dérivées partielles écrites.

Dans le cas d’une fonction de deux variables, la fonction f s’obtient par deux quadratures.