Pour résoudre l’équation
z⁴ + z³ + z² + z + 1 = 0,
on fait la transformation
alors,
est une fonction de z². On écrit

et on résout l’équation

qui est équivalente à l’équation
y² + y – 1 = 0,
dont les racines sont

Par suite,

En remplaçant y par on arrive finalement à

et l’on peut achever la résolution.

La transformation

est fructueuse chaque fois qu’on l’applique à une équation dont les termes équidistants des extrêmes sont égaux ou opposés, c’est-à-dire à une équation réciproque, et elle conduit à la résolution d’une équation de degré moitié.

On montre ainsi, par exemple, que

Relations entre les coefficients et les racines

Toute équation à coefficients réels ou complexes et de degré n admet n racines réelles ou complexes. Si l’équation s’écrit
a₀zⁿ + a₁z^n – 1 + ... + a_pz^n – p +... + a_n = 0, a₀ ≠ 0,
les racines z₁, z₂, ... z_n sont liées aux coefficients a₀, a₁, ..., a_p, ..., a_n par les relations :

La première de ces égalités fait intervenir la somme des racines, la deuxième la somme des produits deux à deux, ..., la p^ième la somme des produits p à p, ..., la dernière le produit des racines. Ces relations sont utiles quand on veut résoudre une équation dont les racines sont assujetties à une condition.

Exemple. Résoudre l’équation
8 x³ – 12 x² – 2 x + 3 = 0,
sachant que ses racines sont en progression arithmétique. Les racines étant désignées par a, b et c, et la raison de la progression par r, b = a + r et c = a + 2 r ; la première des relations entre les coefficients et les racines,

donne

d’où

On achève la résolution soit en utilisant les deux autres relations,

et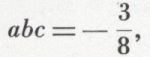

soit en factorisant. Mais, en l’absence de toute condition supplémentaire imposée aux racines, le système des n relations entre les coefficients et les racines est équivalent à l’équation dont il provient, et résoudre l’un, c’est résoudre l’autre. Aucun des deux n’est privilégié. Il serait donc illusoire de remplacer l’équation proposée par le système des relations entre les coefficients et les racines.

Nombres et entiers algébriques

Un élément α appartenant à un surcorps K′ d’un corps K est algébrique sur K′ s’il existe au moins une expression de la forme
a₀ αⁿ + a₁ α^n – 1 + ... + a_n = 0, a₀ ≠ 0,
tous les a_i appartenant au corps K.

Autrement dit, α est racine d’une équation algébrique sur K. De façon plus restrictive, α est un entier algébrique sur K si le coefficient a₀ est égal à 1. Si K est le corps ℚ des rationnels et K′ le corps ℝ des réels, les nombres algébriques réels sont les nombres réels qui vérifient une équation algébrique à coefficients rationnels et donc entiers, après réduction au même dénominateur et suppression de ce dénominateur. Ces nombres sont appelés nombres algébriques (sans plus). Ainsi est algébrique, car ce qui montre que vérifie l’équation x² – 2 = 0 ; est donc aussi un entier algébrique ; de même est algébrique ; ou encore est algébrique ; en effet, ou  ; d’où (α² – 5)² = 24, ce qui s’écrit aussi α⁴ – 10 α² + 1 = 0.

Les nombres algébriques forment un corps dénombrable, c’est-à-dire un corps dont les éléments peuvent être mis en correspondance biunivoque avec les entiers naturels 1, 2, ... S’il est impossible de trouver une équation à coefficients dans K et non tous nuls, dont α soit racine, l’élément α est dit « transcendant sur K ». Si K est le corps ℚ des rationnels et K′ le corps ℝ des réels, un nombre réel transcendant sur ℚ est dit « transcendant » (sans plus).

Les nombres π, rapport de la longueur d’une circonférence à son diamètre, et e, base des logarithmes népériens, sont transcendants : ils ne sont racines d’aucune équation à coefficients rationnels non nuls.

La transcendance de e a été établie en 1873 par Charles Hermite, celle de π en 1882 par Ferdinand von Lindemann.

E. S.

➙ ℂ / ℚ / ℝ.

 P. Dubreil et M.-L. Dubreil-Jacotin, Leçons d’algèbre moderne (Dunod, 1961). / S. Mac Lane et G. Birkhoff, Algebra (New York et Londres, 1967).