algèbre (suite)
• Au xve s., l’Italien Luca Pacioli (v. 1445 - v. 1514), en 1494, et le Français Nicolas Chuquet (v. 1445 - v. 1500), en 1484, résolvent de nombreux systèmes d’équations affines. Le premier emploie, comme Diophante, une inconnue privilégiée, la cosa, à laquelle il en adjoint parfois une seconde, la quantita. Chuquet procède de même. Il ne donne pas de noms aux deux inconnues, mais il les note 11 et 12. D’autre part, il utilise avec habileté le zéro et les nombres négatifs, rejoignant ainsi les mathématiciens chinois et hindous. Cependant, au xiiie s., Léonard de Pise (v. 1175 - apr. 1240) a fait, lui aussi, quelques pas dans cette voie.
• Le xvie s. apporte dans le domaine des problèmes affines des progrès appréciables, avec, cependant, un certain recul pour l’emploi des nombres négatifs. Michael Stifel (1487-1567) utilise une inconnue privilégiée, notée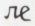 
, mais il lui adjoint, s’il le faut, d’autres inconnues, qu’il désigne par des lettres majuscules A, B, etc. Il dispose des signes + et – pour l’addition et la soustraction. Dus à Johann Widmann d’Eger (xve s.), ces deux signes datent de 1489. Les Français et les Italiens utilisent quant à eux p et m. Les signes d’égalité apparaissent en 1557 chez l’Anglais Robert Recorde (v. 1510-1558) qui l’écrit =, en 1559 chez le Français Johannes Buteo (1492-1572), dont le véritable nom était Jean Bourrel et qui le représente par le symbole [ , enfin en 1637 chez René Descartes (1596-1650), qui adopte le signe 
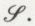C’est le symbole de Recorde qui a prévalu.
Avec Michael Stifel, Jacques Peletier du Mans (1517-1582) et Bourrel, la technique de résolution des systèmes d’équations affines rejoint enfin à peu près le niveau chinois. Chez Bourrel, par exemple, le système
s’écrit :
Le xviie s. apportera peu à la théorie des équations affines, si ce n’est le secours du calcul littéral de François Viète (1540-1603) et de Descartes. Cependant, Gottfried Wilhelm Leibniz (1646-1716) entrevoit le calcul matriciel. C’est Gabriel Cramer (1704-1752) qui fait, en 1750, la première étude approfondie des systèmes d’équations. Avec le xixe s. apparaissent le calcul des déterminants, puis le calcul matriciel. Les espaces vectoriels et toute l’algèbre linéaire ont ici une de leurs origines.
Le second degré
Les équations du second degré remontent aux Babyloniens. Leur technique de résolution est identique à celle que nous utilisons encore. Les seules différences sont que les nombres négatifs ne sont pas utilisés et que les calculs se font dans l’anneau des nombres exprimables d’une façon finie en base 60. L’équation
ax2 + bx + c = 0
n’est donc possible que si les calculs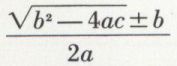
sont exécutables dans cet anneau. Il n’existe aucune notation algébrique, et tout se présente sous forme de problèmes. Les Grecs ont fait de la résolution des équations quadratiques le fondement même de leur géométrie. Les calculs babyloniens sont alors remplacés par des constructions à la règle et au compas, ce qui étend beaucoup les cas de possibilité. Mais les algébristes grecs, comme Diophante, qui opèrent seulement dans l’ensemble ℚ+ des nombres rationnels positifs, sont beaucoup plus gênés que les géomètres. Toute l’analyse indéterminée diophantienne a sa source dans ces difficultés : elle utilise des équations indéterminées où certaines expressions doivent être des carrés parfaits dans le corps ℚ. C’est dans des exercices d’une difficulté inouïe auxquels se livre Diophante en la circonstance que des hommes comme Raffaele Bombelli, mort peu après 1572, Viète ou Simon Stevin (1548-1620) trouveront à la Renaissance une partie importante de leur inspiration.
D’autre part, les géomètres, partant d’une longueur prise comme unité, construisent et étudient d’autres longueurs dérivées, les binômes, de mesure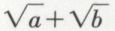
(a et b rationnels), ou les apotomes, de mesure
Tout le livre X des Éléments d’Euclide (iiie s. av. J.-C.) est consacré à une telle étude, qui conduira les algébristes ultérieurs aux quantités irrationnelles quadratiques, ou nombres sourds. C’est à ce courant que l’on doit les mots binôme, trinôme, polynôme. Les Éléments d’Euclide, bien connus en Occident depuis le xiie s., masquaient, sous un habillement géométrique, la résolution des équations. Sous son aspect numérique, celle-ci nous fut dévoilée par les traductions latines des mathématiciens arabes, singulièrement par l’ouvrage de Gherardo da Cremona (v. 1114-1187) Liber Maumeti filii Moysi Alchoarismi de algebra et almuchabala.
Le nom complet de l’auteur arabe Muḥammad ibn Mūsā al-Khārezmi, du début du ixe s., a donné naissance au mot algorithme, qui, réservé d’abord au calcul à la plume avec chiffres arabes, en tant qu’opposé au calcul sur l’abaque, a pris depuis le sens très large de « procédé calculatoire systématique ». Quant à al-djabr, d’où vient le mot algèbre, c’est la transposition d’un terme négatif d’un membre de l’équation dans l’autre membre, al-muqābala étant la réduction des termes semblables.
Le troisième et le quatrième degré
Si l’on trouve quelques équations cubiques chez les Babyloniens et si Archimède (287-212 av. J.-C.) discute au livre II de la Sphère et du cylindre, par des procédés topologiques, les problèmes du troisième degré, c’est l’école italienne du xvie s. qui apporte enfin la résolution des équations du troisième et du quatrième degré. Les inventeurs sont pour le troisième degré Scipione dal Ferro (1465-1526), Niccolo Tartaglia (v. 1499-1557) et Jérôme Cardan (1501-1576), et, pour le quatrième degré, Ludovico Ferrari (1522-1565). Le procédé de résolution se résume, pour nous, à ceci : on ramène l’équation à la forme
x3 + px + q = 0.
On remplace l’inconnue par la somme de deux autres :
x = u + v.
On pose
les quantités u3 et v3 sont calculées par une équation du second degré, et l’on obtient alors les valeurs des termes u, v et x. Ferrari montre, bientôt après, que les équations du quatrième degré se ramènent à celles du troisième.