Sculpteur et architecte italien (Bologne 1595 - Rome 1654).

Algardi apprit le dessin dans sa ville natale, à l’académie de Lodovico Carracci. Après avoir passé quelques années à Mantoue, au service du duc Ferdinand, il arriva à Rome en 1625. Pendant cette période de jeunesse, il se fit surtout connaître par des ouvrages de petit format ; ivoires ou modèles d’orfèvrerie. Sa première commande importante fut celle des deux statues en stuc de Saint Jean-Baptiste et de Sainte Madeleine pour S. Silvestro al Quirinale, vers 1628, époque à laquelle remonte aussi sa production de bustes. Mais la partie la plus brillante de sa carrière coïncide avec le pontificat d’Innocent X (1644-1655), qui fit de lui son sculpteur officiel après la disgrâce du Bernin*. Les principaux ouvrages de ces années sont : la Décapitation de saint Paul, groupe de deux statues de marbre, commande du cardinal Spada, à S. Paolo de Bologne ; Saint Philippe Neri et un ange, groupe de marbre, à S. Maria in Vallicella de Rome ; l’effigie en bronze d’Innocent X, commande du sénat romain, au palais des Conservateurs du Capitole ; le tombeau de Léon XI, à Saint-Pierre de Rome, groupant trois figures de marbre : celle du pape assis et deux Vertus ; enfin, dans la même église, le grand relief de marbre représentant la Rencontre de saint Léon et d’Attila.

La gloire du Bernin ne doit pas faire oublier les autres sculpteurs de l’école romaine du xvii^e s., parmi lesquels Algardi occupe la première place. Son style ample et vigoureux relève du grand mouvement baroque, tout en portant la marque d’une personnalité bien accusée. Au dynamisme, au brio, à l’envolée du Bernin, Algardi oppose une manière non pas plus froide, mais plus calme, une préférence générale pour les compositions statiques ou exprimant au moins un équilibre de forces. Cela reste vrai même du théâtral et puissant haut-relief de Saint-Pierre de Rome, son ouvrage le plus célèbre, mais non le plus révélateur de son tempérament. Il est significatif qu’Algardi ait eu des relations amicales avec des artistes tels que le sculpteur Duquesnoy*, les peintres Dominiquin (v. académisme), Poussin* ou Andrea Sacchi, les uns et les autres réprésentant une tendance classique au sein du baroque romain. Le style d’Algardi, d’autre part, est plus analytique que celui du Bernin ; la virtuosité dans le travail du marbre ou du bronze sert une attention méticuleuse au détail, qu’il s’agisse des visages ou des vêtements. Ces qualités réunies font la valeur des bustes sculptés par Algardi : par exemple, ceux de Panfilo et d’Olimpia Pamphili (palais Doria-Pamphili à Rome) ou celui de Francesco Bracciolini (Victoria and Albert Museum à Londres).

L’activité d’Algardi comme architecte est loin d’être négligeable ; là aussi, il se montre adepte d’un baroque tempéré. Outre le dessin pour la façade de S. Ignazio, à Rome, on lui doit notamment, aux portes de la ville, le Casino di Allegrezza, élevé pour le prince Camillo Pamphili, neveu d’Innocent X, dans les jardins de la villa Doria-Pamphili. Ce pavillon d’agrément offre des volumes simples, dans la tradition de la Renaissance ; son air de fête lui vient de la richesse des façades, décorées de bustes et de bas-reliefs provenant de sarcophages antiques.

B. de M.

Étude des ensembles munis de lois de composition, opérations finies ou relations finies.

S’appuyant simplement sur la logique et la théorie des ensembles, l’algèbre moderne constitue une section majeure des mathématiques, qui ne fut primitivement qu’une partie de l’arithmétique pratique ou logistique. Bien avant que le nom d’algèbre fût créé, se développa une technique de résolution des problèmes qui aboutit d’abord à des recettes stéréotypées, puis à une théorie des équations. Cet art développa peu à peu un système de notations tachygraphiques qui donna, à la fin du xvi^e s., une logistique spécieuse, ou calcul littéral. En même temps, les ensembles sur lesquels travaillait l’algébriste s’élargissaient, dans un but de simplification et de généralisation des procédés opératoires, passant de l’ensemble des nombres entiers naturels ℕ à celui des nombres rationnels positifs ℚ⁺, puis à des extensions quadratiques de ce dernier ensemble et, vers la même époque (xvi^e s.), à quelque chose qui était l’ensemble ℝ des nombres réels, et peu après à l’ensemble ℂ des nombres complexes, etc. Le vocabulaire actuel, trop précis, trahit un peu cette évolution. Cela est d’ailleurs inévitable, le cours historique des mathématiques allant de l’instinctif et du confus vers toujours plus de précision et de clarté.

Problèmes affines

On trouve dans le Papyrus Rhind (v. 1800 av. J.-C.) et dans des tablettes babyloniennes de la même époque des problèmes qui se ramènent pour nous à l’équation ax = b, où a et b sont des nombres rationnels positifs et x une inconnue à déterminer. Ce sont pour les Égyptiens, qui ne disposaient pas de notre calcul des fractions, des questions fort difficiles, telle celle-ci : Quand le scribe te dit 10 est les 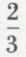et le de quoi ? Sa mise en équation conduit à

La marche de l’ancien calculateur ne peut être que du type, dit « de la fausse position » : si l’on prend 30, les font 20, le dixième 3, et le total 23. Or, comme l’on veut 10, par quoi faut-il multiplier 23 pour avoir 10 ? C’est un premier procédé d’analyse, que l’on trouve très nettement mis en évidence dans un ouvrage chinois, Neuf Chapitres sur l’Art du calcul. Dans le problème égyptien qui vient d’être cité, la seule difficulté de la mise en équation consistait dans la détermination de a, b étant donné par l’énoncé. Des problèmes un peu plus compliqués où ni a ni b ne sont mis en évidence exigent non plus la fausse position simple, mais bien la fausse position double.

Tout cela est nettement exposé dans les Neuf Chapitres. On donne à x deux valeurs arbitraires ; la quantité ax – b prend alors deux valeurs différentes, les erreurs, et l’on fait une interpolation linéaire pour trouver la solution. Répandue par les Arabes, la technique des fausses positions persista en Occident sous le nom arabe d’al-Khatayn (« la chinoise »). On l’utilise toujours lorsqu’on fait une interpellation linéaire, dans une table numérique par exemple. Mais l’ouvrage chinois apporte bien plus. Dans un chapitre réservé au calcul sur l’échiquier apparaît une technique élégante de la résolution des équations linéaires à plusieurs inconnues. Les nombres sont marqués par des jonchets de couleur. Les nombres négatifs apparaissent, représentés par des jonchets noirs. La méthode de résolution s’apparente étrangement au calcul par déterminants. Les algébristes chinois utilisaient les fractions générales et les nombres négatifs, et effectuaient des calculs dans le corps tout entier ℚ des nombres rationnels. L’Occident mettra très longtemps pour atteindre ce stade. Il n’y eut, semble-t-il, aucune influence chinoise sur cette évolution. Nous la reprenons à partir de Diophante d’Alexandrie (iii^e s. apr. J.-C.). Les problèmes affines ne jouent en réalité qu’un rôle mineur dans ses Arithmétiques, ouvrage consacré à l’algèbre sur le corps ℚ⁺ des nombres rationnels positifs, et particulièrement à l’analyse indéterminée, ou diophantienne. Diophante traite de problèmes à plusieurs inconnues, parmi lesquelles il en distingue une, le Nombre, pour laquelle il dispose du symbole Pour la soustraction il emploie le symbole C’est avec ce symbolisme réduit qu’il transforme très habilement ses équations. Son ouvrage n’a d’ailleurs joué un rôle, chez nous, qu’à la fin du xvi^e s.